练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．运行程序如图所示，规定：从“输入一个值x”到“结果是否＞95”为一次程序操作，如果程序操作进行了二次便停止，求x的取值范围．

    分析 根据运算程序，第一次运算结果小于等于95，第二次运算结果大于95列出不等式组，然后求解即可．

    解答 解：由题意得$\left\{\begin{array}{l}{2x+1≤95①}\\{2（2x+1）+1＞95②}\end{array}\right.$，
    解不等式①得，x≤47，
    解不等式②得，x＞23，
    故x的取值范围是23＜x≤47．

    点评 本题考查了一元一次不等式组的应用，读懂题目信息，理解运行程序，列出不等式组是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

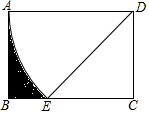    17．如图，在矩形ABCD中，AB=$\sqrt{3}$，AD=2，以D为圆心，AD为半径画弧交线段BC于E，则阴影部分的面积为$\frac{3\sqrt{3}}{2}$-$\frac{2}{3}$π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算：
    （1）4$\frac{11}{12}$-$\frac{7}{8}$+0.125
    （2）$2\frac{5}{6}÷\frac{34}{9}×\frac{1}{18}$
    （3）2$\frac{1}{3}$×6$\frac{3}{4}$-2$\frac{1}{3}$÷1$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．解方程：
    （1）2x-5+4x=5x-3
    （2）$\frac{5x+1}{3}$-$\frac{2x-1}{6}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

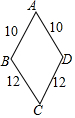    16．如图为两根长度均为10cm和两根长度均为12cm的木条组成的木框，为保证稳定要在BD间加一根木条．设该木条的长为xcm，则x的取值范围是（　　）
    A．0＜x＜20B．2＜x＜20C．0＜x＜24D．2＜x＜24

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．（1）因式分解：2a3-8a2+8a；
    （2）解分式方程：$\frac{x-2}{x+2}$-1=$\frac{16}{{x}^{2}-4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图1，是全国最大的瓷碗造型建筑坐落于江西景德镇，整体造型概念来自“宋代影青斗笠碗”，造型庄重典雅，象征“万瓷之母”．小敏为了计算该建筑物的横断面（瓷碗横断面ABCD为等腰梯形）的高度如图2，她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为45°，而后沿着一段坡度为0.44的小坡PQ步
    行到点Q（此过程中AD、AP、PQ始终处于同一平面）后测得点D的仰角减少了5°．已知坡PQ的水平距离为20米，小敏身高忽略不计．
    （1）试计算该瓷碗建筑物的高度？
    （2）小敏测得AD与水平面夹角约为58°，底座直径AB约为20米，试计算碗口CD的直径为多少米？
    坡度：坡与水平线夹角的正切值．参考数据：sin40°≈0.64，tan40°≈0.84，sin58°≈0.85，tan58°≈1.60．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）$\frac{4-{x}^{2}}{{x}^{2}}$•$\frac{1}{x+2}$+$\frac{2}{x}$          
    （2）（x-2-$\frac{5}{x+2}$）÷$\frac{{x}^{2}-6x+9}{{x}^{2}+2x}$-$\frac{3x}{x-3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．已知一个角的余角为49°26′，那么这个角的补角是139°26′．

    查看答案和解析>>

    同步练习册答案