
【题目】如图,矩形的边OA在x轴上,边OC在y轴上,点B的坐标为(10,8),沿直线OD折叠矩形,使点A正好落在BC上的E处,E点坐标为(6,8),抛物线y=ax2+bx+c经过O、A、E三点.
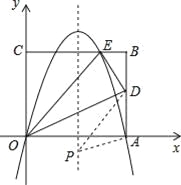

(1)求此抛物线的解析式;
(2)求AD的长;
(3)点P是抛物线对称轴上的一动点,当△PAD的周长最小时,求点P的坐标.
【答案】(1)y=![]() ;(2)AD=5;(3)(5,
;(2)AD=5;(3)(5,![]() )
)
【解析】
试题(1)利用矩形的性质和B点的坐标可求出A点的坐标,再利用待定系数法可求得抛物线的解析式;(2)设AD=x,利用折叠的性质可知DE=AD,在Rt△BDE中,利用勾股定理可得到关于x的方程,可求得AD的长;(3)由于O、A两点关于对称轴对称,所以连接OD,与对称轴的交点即为满足条件的点P,利用待定系数法可求得直线OD的解析式,再由抛物线解析式可求得对称轴方程,从而可求得P点坐标.
试题解析:(1)∵四边形ABCD是矩形,B(10,8),
∴A(10,0), 又抛物线经过A、E、O三点,把点的坐标代入抛物线解析式可得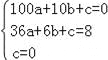 ,解得
,解得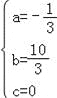 , ∴抛物线的解析式为y=﹣
, ∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x;
x;
(2)由题意可知:AD=DE,BE=10﹣6=4,AB=8, 设AD=x,则ED=x,BD=AB﹣AD=8﹣x,
在Rt△BDE中,由勾股定理可知ED2=EB2+BD2,即x2=42+(8﹣x)2,解得x=5, ∴AD=5;
(3)∵y=﹣![]() x2+
x2+![]() x, ∴其对称轴为x=5, ∵A、O两点关于对称轴对称, ∴PA=PO,
x, ∴其对称轴为x=5, ∵A、O两点关于对称轴对称, ∴PA=PO,
当P、O、D三点在一条直线上时,PA+PD=PO+PD=OD,此时△PAD的周长最小,
如图,连接OD交对称轴于点P,则该点即为满足条件的点P,
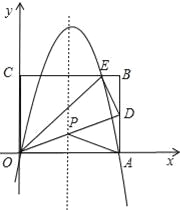
由(2)可知D点的坐标为(10,5),
设直线OD解析式为y=kx,把D点坐标代入可得5=10k,解得k=![]() , ∴直线OD解析式为y=
, ∴直线OD解析式为y=![]() x,
x,
令x=5,可得y=![]() , ∴P点坐标为(5,
, ∴P点坐标为(5,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图乙,![]() 和
和![]() 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形,![]() ,点P为射线BD,CE的交点.
,点P为射线BD,CE的交点.
![]() 如图甲,将
如图甲,将![]() 绕点A旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是______.
绕点A旋转,当C、D、E在同一条直线上时,连接BD、BE,则下列给出的四个结论中,其中正确的是______.
![]()
![]() 若
若![]() ,
,![]() ,把
,把![]() 绕点A旋转,
绕点A旋转,
![]() 当
当![]() 时,求PB的长;
时,求PB的长;
![]() 求旋转过程中线段PB长的最大值.
求旋转过程中线段PB长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条抛物线![]() 与
与![]() 的两个交点
的两个交点![]() 、
、![]() 都在
都在![]() 轴上,抛物线
轴上,抛物线![]() 的顶点为
的顶点为![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)在![]() 轴正半轴上有一点
轴正半轴上有一点![]() ,当
,当![]() 时,求
时,求![]() 的面积;
的面积;
(3)判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使点
,使点![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到点
,得到点![]() 恰好落在抛物线
恰好落在抛物线![]() 上?若存在,求出点
上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
问题情境:在矩形ABCD中,点E为BC边的中点,将△ABE沿直线AE翻折,使点B与点F重合,直线AF交直线CD于点G.
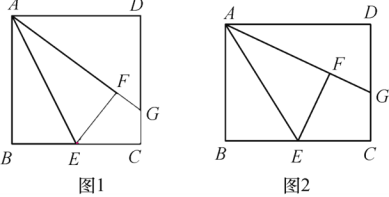
特例探究 实验小组的同学发现:
(1)如图1,当AB=BC时,AG=BC+CG,请你证明该小组发现的结论;
(2)当AB=BC=4时,求CG的长;
延伸拓展:(3)实知小组的同学在实验小组的启发下,进一步探究了当AB∶BC=![]() ∶2时,线段AG,BC,CG之间的数量关系,请你直接写出实知小组的结论:___________.
∶2时,线段AG,BC,CG之间的数量关系,请你直接写出实知小组的结论:___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
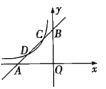
【题目】如图,已知直线![]() 与x轴、y轴分别交于点A,B,与双曲线
与x轴、y轴分别交于点A,B,与双曲线![]() 分别交于点C,D,且点C的坐标为
分别交于点C,D,且点C的坐标为![]() .
.
(1)分别求出直线、双曲线的函数表达式.
(2)求出点D的坐标.
(3)利用图象直接写出:当x在什么范围内取值时![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
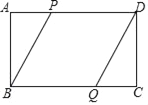
【题目】如图,矩形ABCD中,点P是线段AD上任意一点,点Q为BC上一点,且AP=CQ.
(1)求证:BP=DQ;
(2)若AB=4,且当PD=5时四边形PBQD为菱形.求AD为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
操作与发现:
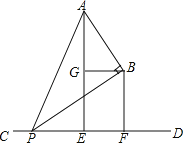
如图,已知A,B两点在直线CD的同一侧,线段AE,BF均是直线CD的垂线段,且BF在AE的右边,AE=2BF,将BF沿直线CD向右平移,在平移过程中,始终保持∠ABP=90°不变,BP边与直线CD相交于点P,点G是AE的中点,连接BG.
探索与证明:求证:
(1)四边形EFBG是矩形;
(2)△ABG∽△PBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
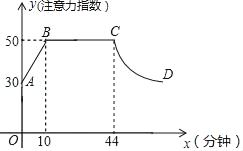
【题目】一般情况下,中学生完成数学家庭作业时,注意力指数随时间x(分钟)的变化规律如图所示(其中AB、BC为线段,CD为双曲线的一部分).
(1)分别求出线段AB和双曲线CD的函数关系式;
(2)若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com