练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．已知：x=$\frac{1}{2+\sqrt{3}}$，y=$\frac{1}{2-\sqrt{3}}$．若x的整数部分是m，y的小数部分是n，求5m5+（x-n）2-y的值．

    分析 先化简x与y的值，再求得m，n的值，代入计算即可．

    解答 解：∵x=$\frac{1}{2+\sqrt{3}}$，y=$\frac{1}{2-\sqrt{3}}$，
    ∴x=2-$\sqrt{3}$，y=2+$\sqrt{3}$，
    ∵x的整数部分是m，y的小数部分是n，
    ∴m=0，n=$\sqrt{3}$-1，
    ∴原式=（2-$\sqrt{3}$-$\sqrt{3}$+1）2-2-$\sqrt{3}$=（3-2$\sqrt{3}$）2-2-$\sqrt{3}$=21-12$\sqrt{3}$-2-$\sqrt{3}$=19-13$\sqrt{3}$．

    点评 本题考查了分母有理化，掌握有理化因式的求法以及无理数整数部分与小数部分的求法是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．如图，已知?OBDC的对角线相交于点E，其中O（0，0），B（6，8），C（m，0），反比例函数y=$\frac{k}{x}$（k≠0）的图象经过点B．
    （1）求k的值；
    （2）若点E恰好落在反比例函数y=$\frac{k}{x}$的图象上，求?OBDC的面积；
    （3）当m=9时，判断反比例函数图象是否经过CD的中点？若经过，请说明理由；若不经过，求出CD与反比例函数图象的交点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，ABC三点在同一条直线上，且∠1=∠2，∠3=∠D，试判断BD与CE的位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

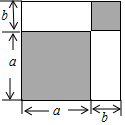    15．请认真观察图形，解答下列问题：
    （1）根据图中条件，用两种方法表示两个阴影图形的面积的和（只表示，不化简）；
    （2）由（1）你能得到怎样的等量关系？请用等式表示；
    （3）如果图中的a、b（a＞b）满足a2+b2=53，ab=14，求a+b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，在网格中的两个全等的图形（阴影部分），用这两个图形拼成轴对称图形，试分别画出两种不同的拼法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图所示，两个村庄B，C之间的距离为BC=15km，村庄D与C之间有一条笔直的公路，全长为14km，BD之间拟建一条公路，测算其直线距离约13km，已知从B修一到公路CD的道路造价至少为600000元，请以上述标准计算出若要修建BD之间的公路最低造价是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图：∠PAC=30°，AD=3，BD=10，以BD为直径的交AP于E、F，求圆心O到AP的距离及EF长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．若|a+1|=2，|b-2|=3，且ab＜0，则a-b=2或-8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．在平面直角坐标系中，顺次连接下列各点，并画出图形．
    （-5，2），（-1，4），（-5，6），（-3，4），（-5，2）
    （1）不改变这些点的纵坐标，将它们的横坐标都乘以-1．写出新的点的坐标；
    （2）在同一坐标系中，描出这些新点，并顺次连接起来；
    （3）新图形与原图形有什么关系？

    查看答案和解析>>

    同步练习册答案