
����Ŀ��ijѧУ��1500��ѧ���μ������Ұ����ǵĿ�����Ϊ�����ͼƬ�������������������ȡ���ֲ���ѧ���ijɼ�����������������ͼ�����£�
Ƶ�ʷֲ�ͳ�Ʊ� | Ƶ�ʷֲ�ֱ��ͼ | ||
������ | Ƶ�� | Ƶ�� |
|
60��x��70 | 40 | 0.40 | |
70��x��80 | 35 | b | |
80��x��90 | a | 0.15 | |
90��x��100 | 10 | 0.10 | |
�����������Ϣ������������⣺
��1������a�� ��b�� ��
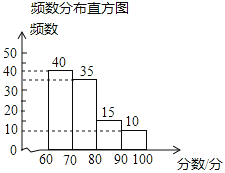
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3������������ɼ�80�����ϣ���80�֣���Ϊ���㣬��ô�������Ƕ��٣����ҹ����У����ѧ����������������
���𰸡���1��a��15��b��0.35����2������ͼ����3��25�G��375
��������
�����������1�����ݵ�һ���Ƶ����Ƶ�ʿ�����ܵĵ���������Ȼ����ݵڶ����Ƶ���͵������Ƶ�ʼ������a��b��ֵ��
��2�����ݣ�1���������aֵ���ɲ�ȫƵ���ֲ�ֱ��ͼ��
��3��������=������͵������Ƶ��֮�͡�100%�������������������ʣ����㼴�ɵý⣮
��1���ܵĵ�������=40��0.40=100�ˣ�
���ڶ����Ƶ��Ϊ35��
��b=35��100=0.35��
���������Ƶ��Ϊ0.15��
��a=100��0.15=15��
��2����ȫƵ���ֲ�ֱ��ͼ������ʾ��

��3��������=��0.15+0.10����100%=25%��
1500��25%=375���ˣ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����κ���y1=(x��2)(x��4)��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����Գ���l��x�ύ�ڵ�C�����Ķ���Ϊ��D��
��1�����D������ ��
��2����P�ڶԳ���l�ϣ�λ�ڵ�C�Ϸ�����CP=2CD����PΪ����Ķ��κ���y2=ax2+bx+c��a��0����ͼ�����A��
����˵�����κ���y2=ax2+bx+c��a��0����ͼ�����B��
�ڵ�R�ڶ��κ���y1=��x��2����x��4����ͼ���ϣ���x��ľ���Ϊd������R������Ϊ ʱ�����κ���y2=ax2+bx+c��a��0����ͼ��������ֻ�������㵽x��ľ������2d��
����ͼ2����֪0��m��2������M��0��m����x���ƽ���ߣ��ֱ��κ���y1=��x��2����x��4��y2=ax2+bx+c��a��0����ͼ���ڵ�E��F��G��H����E��G�ڶԳ���l��ࣩ������H��x��Ĵ��ߣ�����Ϊ��N�������κ���y1=��x��2����x��4����ͼ���ڵ�Q������GHN�ס�EHQ����ʵ��m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
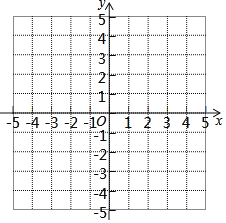
����Ŀ����֪��ƽ��ֱ������ϵ��������A����2��1����B��3��1����C��2��3���������������⣺
��1��������ϵ�����A��B��C��λ�ã�
��2��������ABC����x��ԳƵ�ͼ�Ρ�A1B1C1����д������A1��B1��C1�����ꣻ
��3��д����C�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ�ǡ�ABC����������ֱ���A����3��1����B��0��3����C��0��1��

��1������ABC�Ե�CΪ��ת������ת180�㣬������ת���Ӧ�ġ�A1B1C1��
��2���ֱ�����AB1��BA1�����ı���AB1A1B�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ŀڴ���װ�к졢�ơ���������ɫ��С�����ɸ�������ɫ�������ͬ�������к���2�����ֱ����1�š�2�ţ�������1������������������һ������������ĸ���Ϊ![]() ��
��
��1������л���ĸ�����
��2����һ����������һ�����Żأ����ڶ���������һ�������û���״ͼ���б���ķ�����������������ͬ��ɫ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��ͼ����
��ͼ����![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����֪��
����֪��![]() ����Ϊ
����Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ��
��
��1�����������Ľ���ʽ��һ�κ����Ľ���ʽ��
��2������![]() ����
����![]() �������
�������
��3���۲�ͼ��ֱ��д��![]() ʱ
ʱ![]() ��ȡֵ��Χ������������
��ȡֵ��Χ������������
��4��ֱ��д����![]() Ϊ
Ϊ![]() ����һ���㣬��������
����һ���㣬��������![]() Ϊ����������ʱ��
Ϊ����������ʱ��![]() ����������������
����������������
���� ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
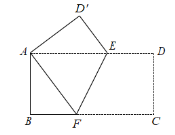
����Ŀ����ͼ����һ�ų�����ֽƬ ABCD �۵�������ʹ��ԽǶ��� A��C �غϣ����䳤 BC Ϊ 9���� AB Ϊ 3��
����֤����AEF �ǵ��������Σ�
��EF= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����۲�˼��������ͼ���߶�AB����������C��D��ͼ�й��� ���߶Σ�
![]()
��2����ģ������������߶�����m���㣨�����߶ε������˵㣩������߶��Ϲ��� ���߶�.���Ҫ˵�����۵���ȷ�ԣ�
��3������չӦ�ã���8λͬѧ�μӰ�����֯������������������õ�ѭ���ƣ���ÿ��λͬѧ֮�䶼Ҫ����һ������������ôһ��Ҫ���� ������.��ȣ�ģ��������Ҫ˵��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��D��E����ABC��BC���ϵ����㣬AD=AE��Ҫ֤����ABE�ա�ACD��Ӧ��������һ��ʲô������������������������ٸ���֤����

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com