
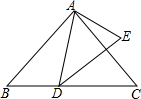
 如图,已知∠BAD=∠CAE,AB•AE=AD•AC.求证:∠C=∠E.
如图,已知∠BAD=∠CAE,AB•AE=AD•AC.求证:∠C=∠E. 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
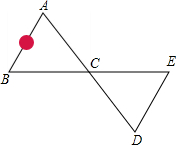 如固,为修筑一条公路,需测量出被大石头阻挡的∠BAC的大小,为此,小张师傅便在直线AC上取点D,使AC=CD,在BC的延长线上取点E,使BC=CE,连接DE,只要测出∠D的度数,则可知∠A的度数等于∠D的度数.请说明理由.
如固,为修筑一条公路,需测量出被大石头阻挡的∠BAC的大小,为此,小张师傅便在直线AC上取点D,使AC=CD,在BC的延长线上取点E,使BC=CE,连接DE,只要测出∠D的度数,则可知∠A的度数等于∠D的度数.请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
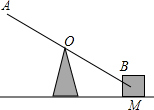 如图,某人在A处利用杠杆抬起位于B处的重物M.已知重物M的质量为50kg,杠杆与地面的夹角为30°,在A处的人和B处的重物与支架的顶端O的水平距离都为3m.试问:该人将重物M抬至水平位置所做的功是多少焦耳(精确到0.1,
如图,某人在A处利用杠杆抬起位于B处的重物M.已知重物M的质量为50kg,杠杆与地面的夹角为30°,在A处的人和B处的重物与支架的顶端O的水平距离都为3m.试问:该人将重物M抬至水平位置所做的功是多少焦耳(精确到0.1,| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com