
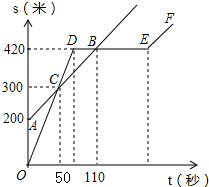
 某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:分析 (1)观察函数图象即可找出谁是自变量谁是因变量;
(2)根据速度=路程÷时间,即可分别算出朱老师以及小明的速度;
(3)根据函数图象即可得到结论.
解答 解:(1)观察函数图象可得出:自变量为小明出发的时间t,因变量为距起点的距离s.
故答案为:小明出发的时间t;距起点的距离s.
(2)朱老师的速度为:(300-200)÷50=2(米/秒);
小明的速度为:300÷50=6(米/秒).
故答案为:2;6.
(3)小明与朱老师相遇2次,相遇时距起点的距离分别为300米或420米,
故答案为:300米或420米.
点评 本题考查了一次函数的应用,观察函数图象找出点的坐标利用待定系数法求出函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
 完成下面的证明.
完成下面的证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,现有一架长4m的梯子AB斜靠在墙面上,要想使人安全地攀上梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.
如图,现有一架长4m的梯子AB斜靠在墙面上,要想使人安全地攀上梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com