
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
【答案】(1)甲、乙两种水果的单价分别是16元、20元;(2)水果商进货甲种水果145千克,乙种水果55千克,才能获得最大利润,最大利润是855元.
【解析】
(1)根据题意可以列出相应的分式方程,求出甲、乙两种水果的单价分别是多少元;
(2)根据题意可以得到利润和购买甲种水果数量之间的关系,再根据甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,可以求得甲种水果数量的取值范围,最后根据一次函数的性质即可解答本题.
(1)设甲种水果的单价是x元,则乙种水果的单价是![]() 元,
元,
![]() ,
,
解得,![]() ,
,
经检验,![]() 是原分式方程的解,
是原分式方程的解,
∴![]() ,
,
答:甲、乙两种水果的单价分别是16元、20元;
(2)设购进甲种水果a千克,则购进乙种水果![]() 千克,利润为w元,
千克,利润为w元,
![]() ,
,
∵甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,
∴![]() ,
,
解得,![]() ,
,
∴当![]() 时,w取得最大值,此时
时,w取得最大值,此时![]() ,
,![]() ,
,
答:水果商进货甲种水果145千克,乙种水果55千克,才能获得最大利润,最大利润是855元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AB为
中,AB为![]() 的直径,C为
的直径,C为![]() 上一点,P是
上一点,P是![]() 的中点,过点P作AC的垂线,交AC的延长线于点D.
的中点,过点P作AC的垂线,交AC的延长线于点D.
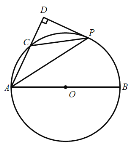
(1)求证:DP是![]() 的切线;
的切线;
(2)若AC=5,![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.
(1)用尺规在边AB上求作一点P,使PC=PB,并连接PC;(不写作法,保留作图痕迹)
(2)当AC=3,BC=4时,△ACP的周长= ;

查看答案和解析>>
科目:初中数学 来源: 题型:
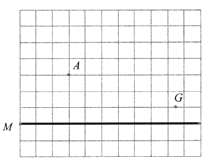
【题目】如图,在每个小正方形的边长为1的网格中,A,M,N均在格点上.在线段![]() 上有一动点B,以
上有一动点B,以![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,使
,使![]() ,
,![]() ,G是一个小正方形边的中点.
,G是一个小正方形边的中点.
(1)当点B的位置满足![]() 时,求此时
时,求此时![]() 的长_______;
的长_______;
(2)请用无刻度的直尺,在如图所示的网格中,画出一个点C,使其满足线段![]() 最短,并简要说明点C的位置是如何找到的(不要求证明)____________.
最短,并简要说明点C的位置是如何找到的(不要求证明)____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
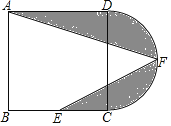
【题目】如图,在正方形ABCD中,![]() ,点E为BC的中点,以CD为直径在正方形外部作半圆CFD,点F为半圆的中点,连接
,点E为BC的中点,以CD为直径在正方形外部作半圆CFD,点F为半圆的中点,连接![]() ,图中阴影部分的面积是( )
,图中阴影部分的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,直线y=2x+2和直线y=![]() x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
A.y=x+2B.y=![]() x+2C.y=4x+2D.y=
x+2C.y=4x+2D.y=![]() x+2
x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AC=BC=m,D是AB边上的一点,将∠B沿着过点D的直线折叠,使点B落在AC边的点P处(不与点A,C重合),折痕交BC边于点E.
(1)特例感知 如图1,若∠C=60°,D是AB的中点,求证:AP=![]() AC;
AC;
(2)变式求异 如图2,若∠C=90°,m=6![]() ,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;
,AD=7,过点D作DH⊥AC于点H,求DH和AP的长;
(3)化归探究 如图3,若m=10,AB=12,且当AD=a时,存在两次不同的折叠,使点B落在AC边上两个不同的位置,请直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: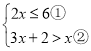 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(1)解不等式①,得: ;
(2)解不等式②得: ;
(3)把不等式①和②的解集在数轴上表示出来;
![]()
(4)原不等式组的解集为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com