
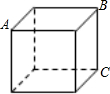
 如图,一只蚂蚁要从正方体得一个顶点A沿表面爬行到顶点B,则沿线段AB爬行,就可以爬行路线最短,这其中的道理是两点之间,线段最短.
如图,一只蚂蚁要从正方体得一个顶点A沿表面爬行到顶点B,则沿线段AB爬行,就可以爬行路线最短,这其中的道理是两点之间,线段最短.  口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
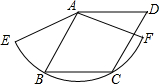 如图,已知菱形ABCD的边长为3 cm,B,C两点在扇形AEF的$\widehat{EF}$上,求$\widehat{BC}$的长度及扇形ABC的面积.
如图,已知菱形ABCD的边长为3 cm,B,C两点在扇形AEF的$\widehat{EF}$上,求$\widehat{BC}$的长度及扇形ABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在矩形ABCD中,AB=2,BC=1,P为矩形ABCD的边上的一个动点,它从点A出发,沿A→B→C运动.设点P经过的路程为x,三角形APC的面积为S.当x等于多少时,三角形APC的面积S等于$\frac{1}{2}$?
已知:如图,在矩形ABCD中,AB=2,BC=1,P为矩形ABCD的边上的一个动点,它从点A出发,沿A→B→C运动.设点P经过的路程为x,三角形APC的面积为S.当x等于多少时,三角形APC的面积S等于$\frac{1}{2}$?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.64a | B. | $\frac{a}{0.8}$ | C. | $\frac{a}{0.64}$ | D. | 0.8a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,DA、CB是⊙O的切线,CD切⊙O于E.
如图,AB是⊙O的直径,DA、CB是⊙O的切线,CD切⊙O于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com