
【题目】在菱形ABCD中,∠BAD=60°
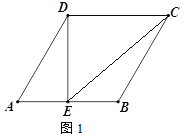
(1)如图1,点E为线段AB的中点,连接DE、CE,若AB=4,求线段EC的长;
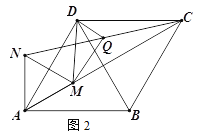
(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论.
【答案】(1)![]() ;(2)见解析;
;(2)见解析;
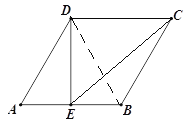
【解析】(1)连接DB,利用菱形的性质、等边三角形的性质及勾股定理即可求解;
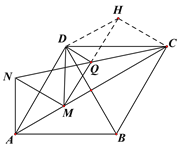
(2)延长MQ到H,使QH=MQ,连接DH、HC ,利用全等三角形的判定和性质、菱形的性质、勾股定理等即可求解.
(1)∵菱形ABCD,
∴AD=DC=AB,DC∥AB,
∴∠DEA=∠CDE,
连接DB,
∵∠BAD=60°,
∴△ADB是等边三角形 ,
∵E为AB中点,
∴DE⊥AB,AE=![]() ,
,
∴∠DEA=90°,
∴∠CDE=90°,
在Rt△ADE中,AD=AB=4,AE=![]() =2,
=2,
∴DE=![]() ,
,
在Rt△DCE中,DC=AB=4,
∴EC=![]() ;
;
(2)延长MQ到H,使QH=MQ,连接DH、HC ,
∵Q为NC中点,
∴NQ=CQ,
∵∠NQM=∠CQH,
∴△NQM≌△CQH(SAS),
∴NM=CH,∠MNQ=∠HCQ,
∴NM∥CH,
∴∠NMA=∠HCM,
∵有等边△AMN,
∴NM=AM,∠NMA=60°,
∴AM=CH,∠HCM=60°,
∵有菱形ABCD,AC为对角线,∠BAD=60°,
∴∠DAM=![]() ,
,
同理,∠DCA=30°,
∴∠HCD=30°,
∴△DAM≌△DCH(SAS),
∴DM=DH,∠ADM=∠CDH,
∴DQ⊥MH,∠MDQ=∠HDQ,∠MDH=∠ADC,
∴∠DQM=90°,
∵有菱形ABCD,∠BAD=60°,
∴∠ADC=120°,
∴∠MDH=120°,
∴∠MDQ=60°,
∴∠DMQ=30°,
∴DM=2DQ.


科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:![]()
第2个等式:![]()
第3等式:![]()
第4个等式:![]()
请解答下列问题:
(1)按以上规律写出第5个等式:a5= = .
(2)用含n的式子表示第n个等式:an= = (n为正整数).
(3)求a1+a2+a3+a4+…+a2018的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9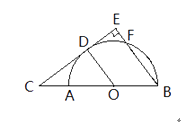
(1)求证:△COD∽△CBE;
(2)求半圆O的半径 ![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;

(2)若体育馆位置坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽水苛公司将“丽水山耕”农副产品运往杭州市场进行销售.记汽车行驶时间为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市?请说明理由:
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
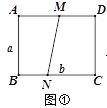
【题目】如图①,矩形纸片ABCD的边长分别为a、b(a<b),点M、N分别为边AD、BC上两点(点A、C除外),连接MN.
(1)如图②,分别沿ME、NF 将MN两侧纸片折叠,使点A、C分别落在MN上的A′、C′处,直接写出ME与FN的位置关系;
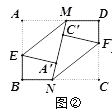
(2)如图③,当MN⊥BC 时,仍按(1)中的方式折叠,请求出四边形A′EBN与四边形C′FDM 的周长(用含a的代数式表示),并判断四边形A′EBN与四边形C′FDM周长之间的数量关系;
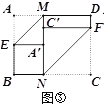
(3)如图④,若对角线BD与MN交于点O,分别沿BM、DN将MN两侧纸片折叠,折叠后,点A、C恰好都落在点O处,并且得到的四边形BNDM是菱形,请你探索a、b之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)写出△ABC各点的坐标.A( , )B( , )C( , ).
(2)若把△ABC向上平移1个单位,再向右平移3个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标.A′( , )B′( , )C′( , ).
(3)连结CA′,CB′,则△CA′B′的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各等式:
13=1=![]() ×11×22
×11×22
13+23=9=![]() ×22×32
×22×32
13+23+33=36=![]() ×32×42
×32×42
…
用你发现的规律解答下列问题:
(1)填空:13+23+33+…+(n﹣1)3+n3=![]() ×( )2×( )2(n为正整数);
×( )2×( )2(n为正整数);
(2)计算:
①13+23+33+…+493+503;
②23+43+63+…+983+1003
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com