
如图所示,等腰梯形ABCD中,AD∥BC,AB=CD
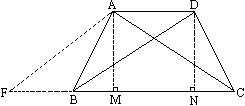
(1)若AD=5,BC=11,梯形的高是4,求梯形的周长;
(2)若AD=a,BC=b,梯形的高是h,梯形的周长为c,则c=________(用含a、b、h的代数式表示,答案直接填在横线上,不要求证明);
(3)若AD=3,BC=7,BD=![]() ,求证:AC⊥BD.
,求证:AC⊥BD.
|
解答和证明: (1)如图所示,过A、D分别作AM⊥BC于M,DN⊥BC于N,则四边形AMND是平行四边形.∴ AD=MN=5,AM=DN=4.又因为 AB=CD,∴ Rt△BAM≌Rt△CDN(HL).∴ BM=CN=由勾股定理得 AB=CD= ∴梯形的周长为 26.(2)c=a+b+ (3)过A作AF∥DB交CB的延长线于F,则四边形ADBF是平行四边形. ∴ AF=BD=AC=∵ BC=7,∴CF=BF+BC=10在△ AFC中,∵ AF2+AC2=(∴ AF⊥AC,∵ AF∥BD,∴AC⊥BD.解析: (1)已知两底的长,要求梯形的周长,关键是求两腰,由于已知高为4,因此分别过A、D两点向BC作垂线,垂足为M、N.则MA=ND=4,MN=AD=5,且Rt△ABM≌Rt△DCN,所以BM=CN=警示误区:证明及推理过程不严密,因果关系混乱是同学们易犯的错误,应注意加强训练. |


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
 如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.
如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.查看答案和解析>>
科目:初中数学 来源: 题型:
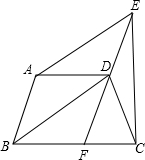 如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.
如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 20、现有5张如图所示的等腰梯形纸片,打算用其中的若干张来拼成较大的等腰梯形,你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.
20、现有5张如图所示的等腰梯形纸片,打算用其中的若干张来拼成较大的等腰梯形,你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,延长BC至点E,使得CE=AD
如图所示,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,延长BC至点E,使得CE=AD查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,
已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com