
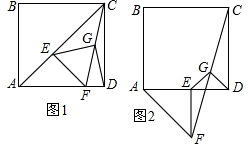
 如图,等腰梯形ABCD,AB∥CD,AB=3$\sqrt{2}$,DC=$\sqrt{2}$,对角线AC⊥BD,平行于线段BD的直线MN、RQ分别以1个单位/秒、2个单位/秒的速度同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G,当直线RQ到达点C时两直线同时停止运动.记等腰梯形ABCD被直线MN扫过的面积为S1,被直线RQ扫过的面积为S2,若S2=mS1,则m的最小值是3.
如图,等腰梯形ABCD,AB∥CD,AB=3$\sqrt{2}$,DC=$\sqrt{2}$,对角线AC⊥BD,平行于线段BD的直线MN、RQ分别以1个单位/秒、2个单位/秒的速度同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G,当直线RQ到达点C时两直线同时停止运动.记等腰梯形ABCD被直线MN扫过的面积为S1,被直线RQ扫过的面积为S2,若S2=mS1,则m的最小值是3. 分析 首先过点C作CK∥BD交AB的延长线于K,易证得四边形DBKC是平行四边形,可求得AK=4$\sqrt{2}$,由四边形ABCD是等腰梯形,可得AC=CK,又由CE=2$\sqrt{2}$且是高,即可证得∠K=∠KCE=∠ACE=∠CAE=45°,继而求得∠AHB的度数,又由等腰直角三角形的性质,求得AC的长,直线移动有两种情况:0<x<$\frac{3}{2}$及$\frac{3}{2}$≤x≤2;然后分别从这两种情况分析求解,注意当0<x<$\frac{3}{2}$时,易得S2=4S1;当$\frac{3}{2}$≤x≤2时,根据相似三角形的性质与直角三角形的面积的求解方法,可求得△BCD与△CRQ的面积,继而可求得S2与S1的值,可得m=-36($\frac{1}{x}$-$\frac{2}{3}$)2+4,然后利用二次函数的性质求得m的变化范围,得最小值.
解答 解:如图1,过点C作CK∥BD交AB的延长线于K,
∵CD∥AB,
∴四边形DBKC是平行四边形,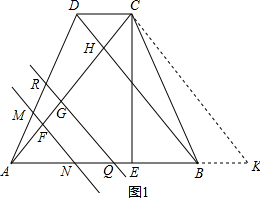
∴BK=CD=$\sqrt{2}$,CK=BD,
∴AK=AB+BK=3$\sqrt{2}$$+\sqrt{2}$=4$\sqrt{2}$,
∵四边形ABCD是等腰梯形,
∴BD=AC,
∴AC=CK,
∴AE=EK=$\frac{1}{2}$AK=2$\sqrt{2}$=CE,
∴CE⊥AB,
∴∠K=∠KCE=∠ACE=∠CAE=45°,
∴∠ACK=90°,
∴∠AHB=∠ACK=90°,
∴AC=AK•cos45°=4$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=4,
直线移动有两种情况:0<x<$\frac{3}{2}$及 $\frac{3}{2}$≤x≤2,如图2,
①当0<x<$\frac{3}{2}$时,
∵MN∥RQ,
∴△AMN∽△ARQ,△ANF∽△AQG,
$\frac{{S}_{1}}{{S}_{2}}$=${(\frac{AG}{AF})}^{2}$=4,
∴S1=4S2;
②当$\frac{3}{2}$≤x≤2时,
∵AB∥CD,
∴△ABH∽△CDH,
∴CH:AH=CD:AB=DH:BH=1:3,
∴CH=DH=$\frac{1}{4}$AC=1,AH=BH=4-1=3,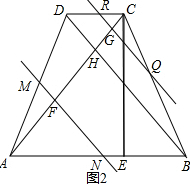
∵CG=4-2x,AC⊥BD,
∴S△BCD=$\frac{1}{2}$×4×1=2,
∵RQ∥BD,
∴△CRQ∽△CDB,
∴S△CRQ=2×($\frac{4-2x}{1}$)2=8(2-x)2,
∵S梯形ABCD=$\frac{1}{2}$(AB+CD)•CE=$\frac{1}{2}$×(3$\sqrt{2}$+$\sqrt{2}$)×2$\sqrt{2}$=8,S△ABD=$\frac{1}{2}$AB•CE=$\frac{1}{2}$×3$\sqrt{2}$×2$\sqrt{2}$=6,
∵MN∥BD,
∴△AMN∽△ADB,
∴$\frac{{S}_{1}}{{S}_{△ABD}}$=${(\frac{AF}{AH})}^{2}$=$\frac{{x}^{2}}{9}$,
∴S1=$\frac{2}{3}$x2,S2=8-8(2-x)2,∵S2=mS1,
∴m=$\frac{{S}_{2}}{{S}_{1}}$=$\frac{8-{8(2-x)}^{2}}{{\frac{2}{3}x}^{2}}$=-$\frac{36}{{x}^{2}}$+$\frac{48}{x}$-12=-36($\frac{1}{x}-\frac{2}{3}$)2+4,
∴m是$\frac{1}{x}$的二次函数,当$\frac{3}{2}$≤x≤2时,即当$\frac{1}{2}$≤$\frac{1}{x}$≤$\frac{2}{3}$时,m随$\frac{1}{x}$的增大而增大,
∴当x=$\frac{3}{2}$时,m最大,最大值为4,
当x=2时,m最小,最小值为3.
故答案为:3.
点评 本题主要考查了相似三角形的判定与性质、等腰梯形的性质、平行四边形的判定与性质、等腰直角三角形的性质以及二次函数的最值问题,注意数形结合、分类讨论思想与函数思想的应用,注意辅助线的作法是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
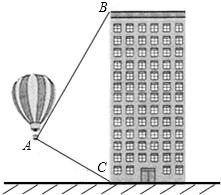 小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度,从热气球探测到此高楼顶部的仰角为66°,此高楼底部的俯角为36°,此时热气球距离C的距离是42米,请计算这栋高楼的高度是多少米(sin66°≈0.90,cos66°≈0.40,tan66°≈2.25,sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
小明和小华准备利用迷你热气球来测量如图所示的高楼BC的高度,从热气球探测到此高楼顶部的仰角为66°,此高楼底部的俯角为36°,此时热气球距离C的距离是42米,请计算这栋高楼的高度是多少米(sin66°≈0.90,cos66°≈0.40,tan66°≈2.25,sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①③ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com