
【题目】如图1,点P是线段AB上的动点(P不与A、B重合),分别以AP、BP为边向线段AB的同侧作等边△APC和等边△BPD,AD和BC交于点M. 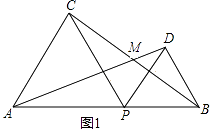
(1)求证:AD=BC;
(2)将点P在线段AB上随意固定,再把△BPD按顺时针方向绕点P旋转一个角度α(α<60°),如图2所示,在旋转过程中,∠AMC的度数是否与α的大小有关?证明你的结论. 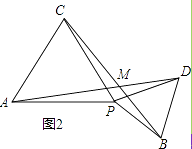
【答案】
(1)解:如图1,
∵△APC和△BPD是等边三角形,
∴CP=AP,DP=PB,∠APC=∠DPB=60°,
∵∠BPC=180°﹣60°,∠DPA=180°﹣60°,
∴∠BPC=∠DPA,
在△BPC和△DPA中,
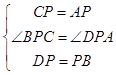 ,
,
∴△BPC≌△DPA,
∴AD=BC
(2)解:∠AMC的度数与α的大小无关,理由如下:
如图2,∵∠BPC=∠CPD+60°,∠DPA=∠CPD+60°,
∴∠BPC=∠DPA,
在△BPC和△DPA中,
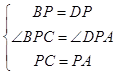 ,
,
∴△BPC≌△DPA,
∴∠BCP=∠DAP,
∴∠AMC=180°﹣∠MCP﹣∠PCA﹣∠MAC
=120°﹣∠BCP﹣∠MAC
=120°﹣(∠DAP+∠MAC)
=120°﹣∠PAC
=60°,
∴∠AMC的度数与α无关.
【解析】(1)只要证明△BPC≌△DPA即可.(2)先证明△BPC≌△DPA得到∠BCP=∠DAP,求出∠AMC的大小即可解决问题.
【考点精析】通过灵活运用等边三角形的性质,掌握等边三角形的三个角都相等并且每个角都是60°即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是【 】
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=27°,则∠B的度数是( ) 
A.84°
B.72°
C.63°
D.54°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度可能是( )
A.第一次右拐15°,第二次左拐165°
B.第一次左拐15°,第二次右拐15°
C.第一次左拐15°,第二次左拐165°
D.第一次右拐15°,第二次右拐15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
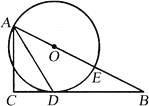
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】俗话说:“水滴石穿”,水滴不断的落在一块石头的同一个位置,经过若干年后,石头上形成了一个深度为0.000000039cm的小洞,则0.000000039用科学记数法可表示为( )
A. 3.9×10﹣8 B. ﹣3.9×10﹣8 C. 0.39×10﹣7 D. 39×10﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2 , 直线l与l1、l2分别交于A、B两点,点M,N分别在l1、l2上,点M,N,P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β. 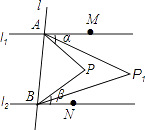
(1)当点P在l1与l2之间时. 求∠APB的大小(用含α、β的代数式表示);
(2)若∠APM的平分线与∠PBN的平分线交于点P1 , ∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 则∠AP1B= , ∠APnB= . (用含α、β的代数式表示,其中n为正整数)
(3)当点P不在l1与l2之间时. 若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2 , …,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn , 请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生物兴趣小组的学生,将自己手机的标本向本组其他成员各赠送意见,全组共赠送了182件,如果全组有x名同学,则根据题意列出的方程是()
A. x ( x+1)=182B. 2x(x+1)=182C. x(x-1)=182D. x(x-1)=182×2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com