
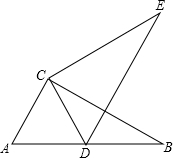
 如图,在直角三角形ABC中,∠ACB=90°,将△ABC绕点C逆时针方向旋转,使点A落在AB边上的点D处,得到△DEC.
如图,在直角三角形ABC中,∠ACB=90°,将△ABC绕点C逆时针方向旋转,使点A落在AB边上的点D处,得到△DEC.分析 (1)根据旋转的定义即可判断;
(2)首先求得∠A=60°,然后根据AC=CD即可证明△ACD是等边三角形;
(3)根据△ACD是等边三角形,可以求得∠ACD=60°,则∠BCD即可求得,进而求得∠BCE.
解答 解:(1)∵将△ABC绕点C逆时针方向旋转,使点A落在AB边上的点D处,得到△DEC.
∴点B的对应点是E,AC对应线段是EC.
故答案为:E,EC;
(2)答:△ACD是等腰三角形.
∵AC=CD,
∴△ACD是等腰三角形;
(3)∵AC=DC,AD=CD,
∴AD=DC=AD,
∴△ACD是等边三角形,
∴∠A=∠ACD=60°,
∵∠ACB=90°,
∴∴∠B=90°-60°=30°,
∴∠ACB=∠DCE,
∴∠BCE=∠ACD=60°.
点评 本题考查了旋转的性质以及等边三角形的判定,旋转前后对应角相等,两个三角形是否成轴对称应看三角形是否全等,对应边沿对称轴折叠后是否重合.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
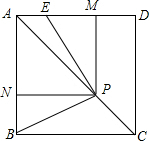 如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
如图,已知正方形ABCD,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
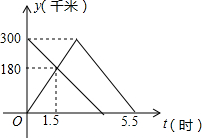 甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.
甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com