
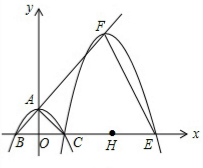
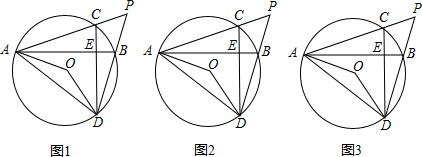
 ��ͼ��������y=ax2+c��a��0����y�ύ�ڵ�A����x�ύ�ڵ�B��C���㣨��C��x���������ϣ�����ABCΪ����ֱ�������Σ������Ϊ4���ֽ���������BA����ƽ�ƣ�ƽ�ƺ�������߾�����Cʱ����x�����һ����ΪE���䶥��ΪF���Գ�����x��Ľ���ΪH��
��ͼ��������y=ax2+c��a��0����y�ύ�ڵ�A����x�ύ�ڵ�B��C���㣨��C��x���������ϣ�����ABCΪ����ֱ�������Σ������Ϊ4���ֽ���������BA����ƽ�ƣ�ƽ�ƺ�������߾�����Cʱ����x�����һ����ΪE���䶥��ΪF���Գ�����x��Ľ���ΪH������ ��1���ɡ�ABCΪ����ֱ�������Σ������Ϊ4�������OA�ij���������õ�A��B��C�����꣬Ȼ���ɴ���ϵ������ô𰸣�
��2���������ֱ��AB�ĺ�������ʽ���趥��F������Ϊ��m��m+2�����������߹���C ��2��0���������ƽ�ƺ�������ߺ�������ʽ���̶���õ�E�����꣬�����ж���OEF�ǵ��������Σ�
��3���ֱ�����һ���ӵ�Q������HF�ϣ�����P��x���Ϸ�ʱ��P��x���·�ʱ���Լ����ζ�����Q������AF�ϣ�ȥ������⼴����ô𰸣�
��� �⣺��1���ߡ�ABCΪ����ֱ�������Σ�
��OA=$\frac{1}{2}$BC��
�֡ߡ�ABC�����=$\frac{1}{2}$BC��OA=4����OA2=4��
��OA=2��
��A��0��2����B��-2��0����C��2��0����
��$\left\{\begin{array}{l}{c=2}\\{4a+c=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=2}\end{array}\right.$��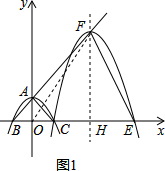 ��2����OEF�ǵ��������Σ��������£����ͼ1��
��2����OEF�ǵ��������Σ��������£����ͼ1��
��A ��0��2������B ��-2��0����
��ֱ��AB�ĺ�������ʽΪ��y=x+2��
�֡�ƽ�ƺ�������߶���F������BA�ϣ�
���趥��F������Ϊ��m��m+2����
��ƽ�ƺ�������ߺ�������ʽΪ��y=-$\frac{1}{2}$��x-m��2+m+2��
�������߹���C ��2��0����
��-$\frac{1}{2}$��x-m��2+m+2=0�����m1=0��m2=6��
��ƽ�ƺ�������ߺ�������ʽΪ��y=-��x-6��2+8��
��y=-$\frac{1}{2}$x2+6x-10��
��y=0ʱ��-$\frac{1}{2}$x2+6x-10=0��
���x1=2��x2=10��
��E��10��0����OE=10��
�֡�F��6��8����OH=6��FH=8��
��OF=$\sqrt{O{H}^{2}+F{H}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10��
��OE=OF������OEFΪ���������Σ�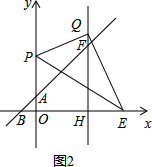 ��3�����ڵ�Q��6��2$\sqrt{21}$����6��3����10��12����4+$\sqrt{14}$��6+$\sqrt{14}$����4-$\sqrt{14}$��6-$\sqrt{14}$����ʹ��P��Q��E����Ϊ��������������POEȫ�ȣ�
��3�����ڵ�Q��6��2$\sqrt{21}$����6��3����10��12����4+$\sqrt{14}$��6+$\sqrt{14}$����4-$\sqrt{14}$��6-$\sqrt{14}$����ʹ��P��Q��E����Ϊ��������������POEȫ�ȣ�
�������£�
��Q��λ�÷��������Σ�
����һ����Q������HF�ϣ�
����P��x���Ϸ�ʱ�����ͼ2��
�ߡ�PQE�ա�POE��
��QE=OE=10��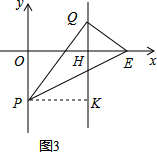 ��Rt��QHE��QH=$\sqrt{Q{E}^{2}-H{E}^{2}}$=$\sqrt{1{0}^{2}-{4}^{2}}$=2$\sqrt{21}$��
��Rt��QHE��QH=$\sqrt{Q{E}^{2}-H{E}^{2}}$=$\sqrt{1{0}^{2}-{4}^{2}}$=2$\sqrt{21}$��
��Q��6��2$\sqrt{21}$����
����P��x���·�ʱ�����ͼ3����PQ=OE=10��
��P����PK��HF�ڵ�K������PK=6��
��Rt��PQK��QK=$\sqrt{P{Q}^{2}-P{K}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8��
�ߡ�PQE=90�㣬
���PQK+��HQE=90�㣮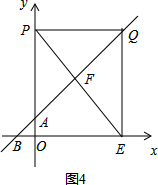 �ߡ�HQE+��HEQ=90�㣬
�ߡ�HQE+��HEQ=90�㣬
���PQK=��HEQ��
�֡ߡ�PKQ=��QHE=90�㣬
���PKQ�ס�QHE��
��$\frac{PK}{QH}=\frac{QK}{HE}$��
��$\frac{6}{QH}=\frac{8}{4}$��
���QH=3��
��Q��6��3���� ���ζ�����Q������AF�ϣ�
���ζ�����Q������AF�ϣ�
��PQ=OE=10ʱ�����ͼ4����QE=PO��
���ı���POEQΪ���Σ�
��Q�ĺ�����Ϊ10��
��x=10ʱ��y=x+2=12��
��Q��10��12����
��QE=OE=10ʱ�����ͼ5��
��Q��QM��y���ڵ�M����E����x��Ĵ��߽�QM�ڵ�N��
��Q��������x��x+2����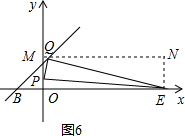 ��MQ=x��QN=10-x��EN=x+2��
��MQ=x��QN=10-x��EN=x+2��
��Rt��QEN����QE2=QN2+EN2��
��102=��10-x��2+��x+2��2��
��ã�x=4��$\sqrt{14}$��
��x=4+$\sqrt{14}$ʱ�����ͼ5��y=x+2=6+$\sqrt{14}$��
��Q��4+$\sqrt{14}$��6+$\sqrt{14}$����
��x=4-$\sqrt{14}$ʱ�����ͼ6��y=x+2=6-$\sqrt{14}$��
��Q��4-$\sqrt{14}$��6-$\sqrt{14}$����
�������������ڵ�Q��6��2$\sqrt{21}$����6��3����10��12����4+$\sqrt{14}$��6+$\sqrt{14}$����4-$\sqrt{14}$��6-$\sqrt{14}$����ʹ��P��Q��E����Ϊ��������������POEȫ�ȣ�
���� �������ڶ��κ������ۺ��⣮�����˴���ϵ����������ʽ��ƽ�Ƶ����ʡ�ȫ�������ε����ʡ����������ε��ж��������Լ����ɶ�����֪ʶ��ע�����շ�������˼���Ӧ�ã�ע��ȷ�����������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��ij��ѧ�С��ѡ������ɽ������AE�ĸߣ�������30m�ߵ�¥CD�ĵײ���D�������A������Ϊ45�㣬��¥��C�������A������Ϊ36��52�䣮��Сɽ��BE=62m��¥�ĵײ�D��ɽ����ͬһˮƽ���ϣ��������ĸ�AE�����ο����ݣ�sin36��52���0.60��tan36��52���0.75��
��ͼ��ʾ��ij��ѧ�С��ѡ������ɽ������AE�ĸߣ�������30m�ߵ�¥CD�ĵײ���D�������A������Ϊ45�㣬��¥��C�������A������Ϊ36��52�䣮��Сɽ��BE=62m��¥�ĵײ�D��ɽ����ͬһˮƽ���ϣ��������ĸ�AE�����ο����ݣ�sin36��52���0.60��tan36��52���0.75���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
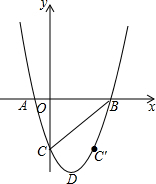 ��֪��������y=x2-4x-m��m��0����x�ύ��A��B���㣬��y�ύ�ڵ�C��DΪ�����ߵĶ��㣬C����������߶Գ���ĶԳƵ�ΪC��㣮
��֪��������y=x2-4x-m��m��0����x�ύ��A��B���㣬��y�ύ�ڵ�C��DΪ�����ߵĶ��㣬C����������߶Գ���ĶԳƵ�ΪC��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
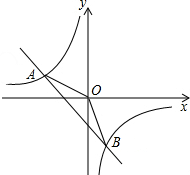 ��ͼ��ʾ��һ�κ���y1=kx+b��ͼ���뷴��������y2=$\frac{m}{x}$��ͼ����A��-2��n����B��1��-3�����㣮
��ͼ��ʾ��һ�κ���y1=kx+b��ͼ���뷴��������y2=$\frac{m}{x}$��ͼ����A��-2��n����B��1��-3�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com