
【题目】(生活观察)甲、乙两人买菜,甲习惯买一定质量的菜,乙习惯买一定金额的菜,两人每次买菜的单价相同,例如:
菜价 | ||
质量 | 金额 | |
甲 |
|
|
乙 |
|
|
菜价 | ||
质量 | 金额 | |
甲 |
| ____元 |
乙 | ____千克 |
|
(1)完成上表;
(2)计算甲两次买菜的均价和乙两次买菜的均价.(均价![]() 总金额总质量)
总金额总质量)
(数学思考)设甲每次买质量为![]() 千克的菜,乙每次买金额为
千克的菜,乙每次买金额为![]() 元的菜,两次的单价分别是
元的菜,两次的单价分别是![]() 元
元![]() 千克、
千克、![]() 元
元![]() 千克,用含有
千克,用含有![]() 、
、![]() 、
、![]() 、
、![]() 的式子,分别表示出甲、乙两次买菜的均价
的式子,分别表示出甲、乙两次买菜的均价![]() 、
、![]() .比较
.比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
(知识迁移)某船在相距为![]() 的甲、乙两码头间往返航行一次,在没有水流时,船的速度为
的甲、乙两码头间往返航行一次,在没有水流时,船的速度为![]() 所需时间为:如果水流速度为
所需时间为:如果水流速度为![]() 时(
时(![]() ),船顺水航行速度为(
),船顺水航行速度为(![]() ),逆水航行速度为(
),逆水航行速度为(![]() ),所需时间为
),所需时间为![]() 请借鉴上面的研究经验,比较
请借鉴上面的研究经验,比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
【答案】【生活观察】:(1)见解析表;(2)甲两次买菜的均价是![]() 元
元![]() 千克:乙两次买菜的均价是
千克:乙两次买菜的均价是![]() 元
元![]() 千克;【数学思考】:当
千克;【数学思考】:当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,见解析;【知识迁移】:
,见解析;【知识迁移】:![]() ,见解析.
,见解析.
【解析】
(1)根据单价、质量与金额的关系,进行求解.(2)根据均价![]() 总金额
总金额![]() 总质量,进行求解.【数学思考】:根据均价
总质量,进行求解.【数学思考】:根据均价![]() 总金额
总金额![]() 总质量,进行表示与大小比较.【知识迁移】:根据时间=路程
总质量,进行表示与大小比较.【知识迁移】:根据时间=路程![]() 速度,进行表示与大小比较.
速度,进行表示与大小比较.
(1)根据单价、质量与金额的关系,可得甲的金额和乙的质量,如图表所示
第二次:
菜价 | ||
质量 | 金额 | |
甲 |
|
|
乙 |
|
|
(2)根据均价![]() 总金额
总金额![]() 总质量,甲两次买菜的均价为
总质量,甲两次买菜的均价为![]() 元
元![]() 千克,乙两次买菜的均价为
千克,乙两次买菜的均价为![]() 元
元![]() 千克.
千克.
【数学思考】
:
![]() ,
,
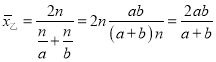 ,
,
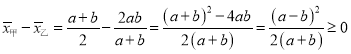 .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
【知识迁移】
:
![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
又![]() ,
,![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中因故停留了一段时间后,仍按原速骑行,小李骑摩托车比小张晚出发一段时间,以800米/分的速度匀速从乙地到甲地,两人距离乙地的路程y(米)与小张出发后的时间x(分)之间的函数图象如图所示.
(1)求小张骑自行车的速度;
(2)求小张停留后再出发时y与x之间的函数表达式;
(3)求小张与小李相遇时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△OAB如图所示放置在平面直角坐标系中,直角边OA与x轴重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB绕点O逆时针旋转90°,点B旋转到点C的位置,抛物线y=ax2+bx经过点C、A.

(1)求该抛物线的解析式;
(2)在x轴上方的抛物线上有一动点P,过点P作x轴的平行线交抛物线于点M,分别过点P,点M作x轴的垂线,交x轴于R、S两点,问:四边形PRSM的周长是否有最大值?如果有,请求出最值,并写出解答过程;如果没有,请说明理由.
(3)在x轴上方的抛物线上是否存在点Q,过点Q作x轴的垂线,垂足为H,使得以O、Q、H为顶点的三角形与OAB相似,如果存在,直接写出点Q的坐标,如果不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
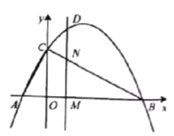
【题目】二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿![]() 方向运动,过点
方向运动,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() ,连接
,连接![]() .设运动的时间为
.设运动的时间为![]() 秒.
秒.
(1)求二次函数![]() 的表达式:
的表达式:
(2)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积:
的面积:
(3)在直线![]() 上存在一点
上存在一点![]() ,当
,当![]() 是以
是以![]() 为直角的等腰直角三角形时,求此时点
为直角的等腰直角三角形时,求此时点![]() 的坐标;
的坐标;
(4)当![]() 时,在直线
时,在直线![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
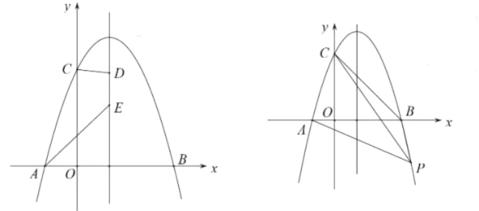
【题目】如图所示抛物线![]() 过点
过点![]() ,点
,点![]() ,且
,且![]()
(1)求抛物线的解析式及其对称轴;
(2)点![]() 在直线
在直线![]() 上的两个动点,且
上的两个动点,且![]() ,点
,点![]() 在点
在点![]() 的上方,求四边形
的上方,求四边形![]() 的周长的最小值;
的周长的最小值;
(3)点![]() 为抛物线上一点,连接
为抛物线上一点,连接![]() ,直线
,直线![]() 把四边形
把四边形![]() 的面积分为3∶5两部分,求点
的面积分为3∶5两部分,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
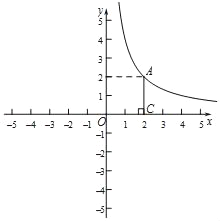
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (x>0)的图象经过点A,作AC⊥x轴于点C.
(x>0)的图象经过点A,作AC⊥x轴于点C.
(1)求k的值;
(2)直线y=ax+b(a≠0)图象经过点A交x轴于点B,且OB=2AC.求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
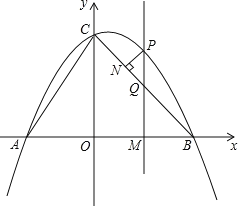
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .点
.点![]() 是第一象限内抛物线上的一个动点,点
是第一象限内抛物线上的一个动点,点![]() 的横坐标为
的横坐标为![]() .
.
(1)求此抛物线的表达式;
(2)过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 交
交![]() 于点
于点![]() .试探究点P在运动过程中,是否存在这样的点
.试探究点P在运动过程中,是否存在这样的点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形.若存在,请求出此时点
为顶点的三角形是等腰三角形.若存在,请求出此时点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .请用含
.请用含![]() 的代数式表示线段
的代数式表示线段![]() 的长,并求出当
的长,并求出当![]() 为何值时
为何值时![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一台起重机,他的机身高AC为21m,吊杆AB长为36m,吊杆与水平线的夹角∠BAD可从30°升到80°.求这台起重机工作时,吊杆端点B离地面CE的最大高度和离机身AC的最大水平距离(结果精确到0.1m). (参考数据:sin80°≈0.98,cos80°≈0.17,tan33°≈5.67,![]() ≈1.73)
≈1.73)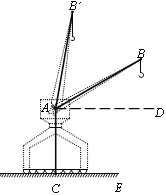
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com