
【题目】已知:∠BAC.
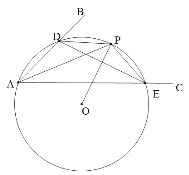
(1)如图,在平面内任取一点O;
(2)以点O为圆心,OA为半径作圆,交射线AB于点D,交射线AC于点E;
(3)连接DE,过点O作线段DE的垂线交⊙O于点P;
(4)连接AP,DP和PE.根据以上作图过程及所作图形,下列四个结论中:
①△ADE是⊙O的内接三角形; ② ![]() ;
;
③ DE=2PE; ④ AP平分∠BAC.
所有正确结论的序号是______________.
【答案】①④
【解析】
①按照圆的内接三角形的定义判断即可,三顶点都在一个圆周上的三角形,叫做这个圆周的内接三角形;
② 利用垂径定理得到弧长之间的关系即可;
③设OP与DE交于点M,利用垂径定理可得DE⊥OP,DE=2ME,再利用直角三角形中斜边长大于直角边,找到PE与与ME的关系,进一步可以得到DE与PE的关系;
④根据![]() ,即可得到∠DAP=∠PAE,则AP平分∠BAC.
,即可得到∠DAP=∠PAE,则AP平分∠BAC.
解:①点A、D、E三点均在⊙O上,所以△ADE是⊙O的内接三角形,此项正确;
② ∵DE⊥DE交⊙O于点P
∴ ![]()
并不能证明![]() 与
与![]() 、
、![]() 关系,
关系,
∴![]() 不正确;
不正确;
③设OP与DE交于点M
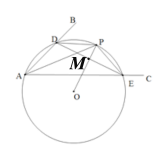
∵DE⊥DE交⊙O于点P
∴DE⊥OP, ME=![]() DE(垂径定理)
DE(垂径定理)
∴△PME是直角三角形
∴ME<PE
∴![]() <PE
<PE
∴DE<2PE
故此项错误.
④∵![]() (已证)
(已证)
∴∠DAP=∠PAE(同弧所对的圆周角相等)
∴AP平分∠BAC.
故此项正确.
故正确的序号为:①④


科目:初中数学 来源: 题型:
【题目】已知AB⊥DE于A,C,O是AB上一点,且AC=CO=OB=2,以O为圆心作扇形BOF,F到直线AB的距离为![]() .
.

(1)求扇形BOF的面积:
(2)将直线DE绕A点旋转得到直线D'E';
①当直线D'E'与扇形BOF相切时,求旋转角的大小;
②设直线D'E'与扇形BOF的弧相交于M、N,若AM=MN,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,根据测试成绩(成绩都不低于50分)绘制出如图所示的部分频数分布直方图.
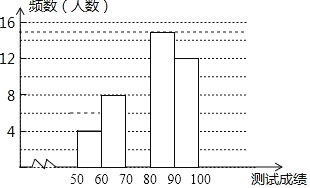
请根据图中信息完成下列各题.
(1)将频数分布直方图补充完整人数;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少;
(3)现将从包括小明和小强在内的4名成绩优异的同学中随机选取两名参加市级比赛,求小明与小强同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.
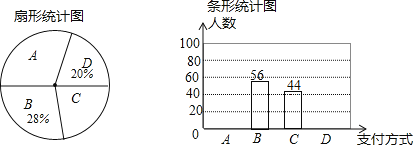
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD对角线AC上的一个动点(点E可以与点A和点C重合),连接BE.已知AB=3cm,BC=4cm.设A、E两点间的距离为xcm,BE的长度为ycm.

某同学根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是该同学的探究过程,请补充完整:
(1)通过取点、画图、测量及分析,得到了x与y的几组值,如下表:

说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:当BE=2AE时,AE的长度约为 cm.(结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海滨浴场有100个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,以此类推,为了投资少而获利大,每个遮阳伞每天应提高_______________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点A逆时针旋转,使点D落在⊙O上,若正方形ABCD的边长和⊙O的半径均为6cm,则点D运动的路径长为( )

A.2πcmB.![]() cmC.πcmD.
cmC.πcmD.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
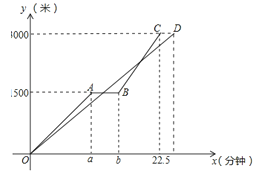
【题目】(2017黑龙江省齐齐哈尔市,第25题,10分)“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人再次选择自行车作为出行工具,小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)a= ,b= ,m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是v米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com