
【题目】如图三角形ABC是圆O的内接正三角形,弦EF经过BC边的中点D,且EF平行AB,若AB等于6,则EF等于________.

【答案】![]()
【解析】
设AC与EF交于点G,由于EF∥AB,且D是BC中点,易得DG是△ABC的中位线,即DG=3;易知△CDG是等腰三角形,可过C作AB的垂线,交EF于M,交AB于N;然后证DE=FG,根据相交弦定理得BDDC=DEDF,而BD、DC的长易知,DF=3+DE,由此可得到关于DE的方程,即可求得DE的长,EF=DF+DE=3+2DE,即可求得EF的长;
解:如图,过C作CN⊥AB于N,交EF于M,则CM⊥EF,

根据圆和等边三角形的性质知:CN必过点O,
∵EF∥AB,D是BC的中点,
∴DG是△ABC的中位线,
即DG=![]() AB=3;
AB=3;
∵∠ACB=60°,BD=DC=![]() BC,AG=GC=
BC,AG=GC=![]() AC,且BC=AC,
AC,且BC=AC,
∴△CGD是等边三角形,
∵CM⊥DG,
∴DM=MG;
∵OM⊥EF,
由垂径定理得:EM=MF,
故DE=GF,
∵弦BC、EF相交于点D,
∴BD×DC=DE×DF,
即DE×(DE+3)=3×3;
解得DE=![]() 或
或![]() (舍去);
(舍去);
∴EF=3+2×![]() =
=![]() ;
;


科目:初中数学 来源: 题型:
【题目】若一条弧经过一个多边形相邻两边中点,并且该弧上所有点都在该多边形的内部或边上,则称该弧为此两边中点连线的EVA弧.例如,图1中,在△ABC中,D,E分别是△ABC两边的中点,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为DE的一条EVA弧.
为DE的一条EVA弧.
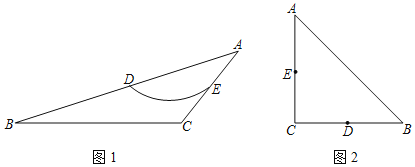
(1)如图2,在Rt△ABC中,∠C=90°,AC=BC=4![]() ,D,E分别是BC,AC的中点,画出DE的最长的EVA弧
,D,E分别是BC,AC的中点,画出DE的最长的EVA弧![]() ,并直接写出此时
,并直接写出此时![]() 的长;
的长;
(2)在平面直角坐标系中,已知点A(0,4),B(0,0),C(4t,0)(t>0),在△ABC中,D,E分别是AB,AC的中点.
①若t=1,求DE的EVA弧![]() 所在圆的圆心P的纵坐标m的取值范围;
所在圆的圆心P的纵坐标m的取值范围;
②若在△ABC中存在一条DE的EVA弧![]() ,使得
,使得![]() 所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
所在圆的圆心P在△ABC的内部或边上,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
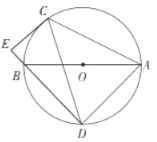
【题目】如图,AB为⊙O的直径,C、D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E.
(1)连接AC、AD,求证:∠DAC+∠ACE=180°.
(2)若∠ABD=2∠BDC,求证:CE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
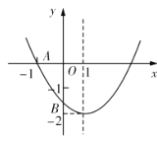
【题目】如图,已知二次函数![]()
![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的交点
轴的交点![]() 在
在![]() 和
和![]() 之间(不包括这两点),对称轴为直线
之间(不包括这两点),对称轴为直线![]() .下列结论:
.下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .
.
其中正确结论有 __________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
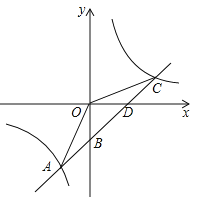
(1) 求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2) 连接OA,OC.求△AOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )
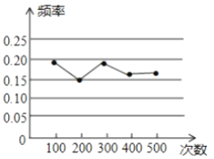
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D.掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
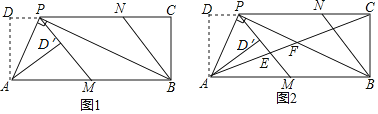
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在边CD上(不与点C,D重合),连接AE,BD交于点F.
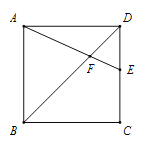
(1)若点E为CD中点,AB=2![]() ,求AF的长.
,求AF的长.
(2)若![]() ∠AFB=2,求
∠AFB=2,求![]() 的值.
的值.
(3)若点G在线段BF上,且GF=2BG,连接AG,CG,设![]() =x,四边形AGCE的面积为
=x,四边形AGCE的面积为![]() ,
,![]() ABG的面积为
ABG的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com