
| A. | 2x•(-xy)2=-2x3y | B. | (-x2)3÷(-x3)2=1 | ||
| C. | ($\frac{3}{4}$a3-$\frac{1}{2}$b)•2ab=$\frac{3}{2}$a4b-ab2 | D. | (3m-1)2=9m2-1 |
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
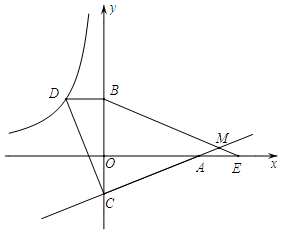 如图,已知点D在反比例函数y=$\frac{m}{x}$的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=$\frac{2}{5}$.
如图,已知点D在反比例函数y=$\frac{m}{x}$的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=$\frac{2}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
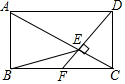 如图,在矩形ABCD中,F是BC边的中点,DF⊥AC,垂足为点E,连接BE,分析下列四个结论:①△CEF∽△CBA;②BE=AB;③AE=2CE;④tan∠ACB=$\sqrt{2}$,其中正确的个数有( )
如图,在矩形ABCD中,F是BC边的中点,DF⊥AC,垂足为点E,连接BE,分析下列四个结论:①△CEF∽△CBA;②BE=AB;③AE=2CE;④tan∠ACB=$\sqrt{2}$,其中正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
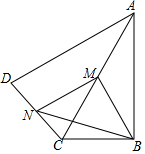 如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校1200名学生参加了全市得到“读数”活动,该校随机选取部分学生,对他们在三、四两个月的读数时间进行调查,并根据调查数据制作统计表和如图所示的频数分布直方图,均不完整,解答下列问题.
某校1200名学生参加了全市得到“读数”活动,该校随机选取部分学生,对他们在三、四两个月的读数时间进行调查,并根据调查数据制作统计表和如图所示的频数分布直方图,均不完整,解答下列问题.| 日人均读书时间x/h | 人数/人 | 百分比 |
| 0≤x≤0.5 | 6 | |
| 0.5<x≤1 | 30 | |
| 1<x≤1.5 | 50% | |
| 1.5<x≤2 | 10 | 10% |
| 2<x≤2.5 | b | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东45°的方向,请求出海岛C到航线AB的距离(结果保留根号).
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东45°的方向,请求出海岛C到航线AB的距离(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com