
【题目】在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.
(1)梯形ABCD的面积等于 .
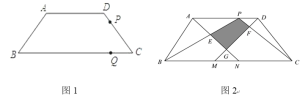
(2)如图1,动点P从D点出发沿DC以DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.当PQ∥AB时,P点离开D点多少时间?
(3)如图2,点K是线段AD上的点,M、N为边BC上的点,BM=CN=5,连接AN、DM,分别交BK、CK于点E、F,记△ ADG和△ BKC重叠部分的面积为S,求S的最大值.
【答案】(1)36;(2)t=![]() ;(3)
;(3)![]()
【解析】
(1)已知梯形各边的长,用勾股定理易求高以及其面积;
(2)本题要找出线段之比,设要用x秒后PQ∥AB,已知![]() ,求出x的值即可;
,求出x的值即可;
(3)过G作GH⊥BC,延长HG交AD于I;过E作EX⊥BC,延长XE交AD于Y;过F作FU⊥BC,延长UF交AD于W;利用相似三角形的性质分别表示出EX和FU的长,再利用![]() 得到相应的关系式,最后通过配方求得S的最大值即可.
得到相应的关系式,最后通过配方求得S的最大值即可.
解:(1)如图,过点D作DE⊥BC于点E,
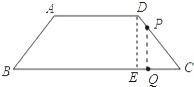
∵AB=DC=5,AD=6,BC=12.
∴由题意可知CE=![]() (BC-AD)=3,
(BC-AD)=3,
在Rt△DEC中,![]() ,
,
∴梯形ABCD的面积为![]() ,
,
故答案为:36;
(2)分别延长BA和CD,交于点N,
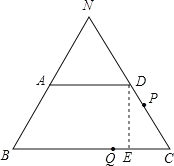
则NA:NB=AD:BC,即
![]()
NA=5,则ND=NA=5.
设用了x秒PQ∥AB,则DP=x,PC=5-x,CQ=2x.
PC:CN=CQ:CB,
![]() ,x=
,x=![]() .
.
即当PQ∥AB时,P点离开D点的时间等于![]() 秒;
秒;
(3)过G作GH⊥BC,延长HG交AD于I;
过E作EX⊥BC,延长XE交AD于Y;
过F作FU⊥BC,延长UF交AD于W;
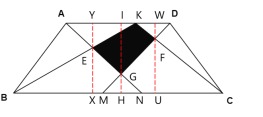
∵AD∥BC,
∴△MGN∽△DGA,
∴ ![]() ,
,
∴HG=1,
设AK=x,
∵AD∥BC,
∴△BEN∽△KEA,
∴![]() ,
,
∴![]() ,
,
同理:![]() ,
,
∴![]()
![]()
![]()
∴当x=3时,![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 |
|
|
| … |
我们把某格中字母和所得到的多项式称为特征多项式,例如:
第1格的“特征多项式”为![]() ;
;
第2格的“特征多项式”为![]() .
.
回答下列问题:
(1)第3格的“特征多项式”为________________,
第4格的“特征多项式”为______________________,
第![]() 格的“特征多项式”为___________________;
格的“特征多项式”为___________________;
(2)若第1格的“特征多项式”的值为![]() ,第2格的“特征多项式”的值为
,第2格的“特征多项式”的值为![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,第![]() 格的特征多项式的值为
格的特征多项式的值为![]() ,则直接写出
,则直接写出![]() 的值;若没有,请说明理由.
的值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
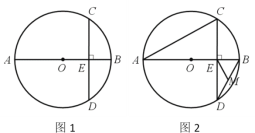
【题目】已知AB是⊙O的直径,C是⊙O上的一点(不与点A,B重合),过点C作AB的垂线交⊙O于点D,垂足为E点.
(1)如图1,当AE=4,BE=2时,求CD的长度;
(2)如图2,连接AC,BD,点M为BD的中点.求证:ME⊥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
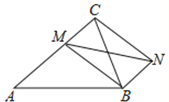
【题目】如图,已知在△ABC中,AB=AC=13,BC=10,点M是AC边上任意一点,连接MB,以MB、MC为邻边作平行四边形MCNB,连接MN,则MN的最小值是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某事业单位组织全体职工参加了“抗击疫情,服务社会”的活动为了了解单位职工参加活动情况,从单位职工中随机抽取部分职工进行调查,统计了该天他们打扫街道、去敬老院服务和社区文艺演出的人数,并绘制了如下不完整的条形统计图和扇形统计图,请根据两幅统计图中的信息,回答下列问题:
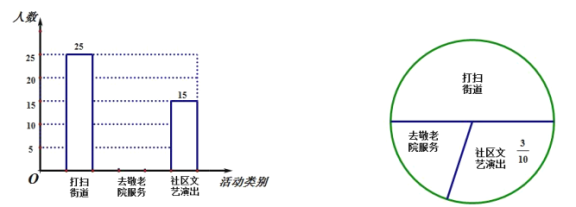
![]() 本次抽样调查共抽取了多少名单位职工?
本次抽样调查共抽取了多少名单位职工?
![]() 通过计算补全条形统计图;
通过计算补全条形统计图;
![]() 若该事业单位共有
若该事业单位共有![]() 名职工,请你估计该单位去敬老院的职工有多少名.
名职工,请你估计该单位去敬老院的职工有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
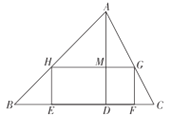
【题目】如图所示,要在底边BC=160cm,高AD=120cm的△ABC铁皮余料上,截取一个矩形EFGH,使点H在AB上,点G在AC上,点E,F在BC上,AD交HG于点M.
(1)设矩形EFGH的长HG=ycm,宽HE=xcm.求y与x的函数关系式;
(2)当x为何值时,矩形EFGH的面积S最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“某市为处理污水,需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时×××××.设原计划每天铺设管道x米,则可得方程![]() .”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
.”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
A.每天比原计划多铺设10米,结果延期20天才完成任务
B.每天比原计划少铺设10米,结果延期20天才完成任务
C.每天比原计划多铺设10米,结果提前20天完成任务
D.每天比原计划少铺设10米,结果提前20天完成任务
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com