
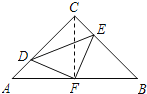
【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC,BC边上运动,且保持AD=CE.连接DE,DF,EF.在此运动变化的过程中,下列结论:

①△DFE是等腰直角三角形;
②四边形CDFE不可能为正方形,
③DE长度的最小值为4;
④四边形CDFE的面积保持不变;
⑤△CDE面积的最大值为8.
其中正确的结论是( )
A.①②③ B.①④⑤ C.①③④ D.③④⑤
【答案】B
【解析】
试题分析:解此题的关键在于判断△DEF是否为等腰直角三角形,作常规辅助线连接CF,由SAS定理可证△CFE和△ADF全等,从而可证∠DFE=90°,DF=EF.所以△DEF是等腰直角三角形.可证①正确,②错误,再由割补法可知④是正确的;
判断③,⑤比较麻烦,因为△DEF是等腰直角三角形DE=![]() DF,当DF与BC垂直,即DF最小时,DE取最小值4
DF,当DF与BC垂直,即DF最小时,DE取最小值4![]() ,故③错误,△CDE最大的面积等于四边形CDEF的面积减去△DEF的最小面积,由③可知⑤是正确的.故只有①④⑤正确.
,故③错误,△CDE最大的面积等于四边形CDEF的面积减去△DEF的最小面积,由③可知⑤是正确的.故只有①④⑤正确.
解:连接CF;
∵△ABC是等腰直角三角形,
∴∠FCB=∠A=45°,CF=AF=FB;
∵AD=CE,
∴△ADF≌△CEF(SAS);
∴EF=DF,∠CFE=∠AFD;
∵∠AFD+∠CFD=90°,
∴∠CFE+∠CFD=∠EFD=90°,
∴△EDF是等腰直角三角形(故①正确).
当D、E分别为AC、BC中点时,四边形CDFE是正方形(故②错误).
∵△ADF≌△CEF,
∴S△CEF=S△ADF∴S四边形CEFD=S△AFC,(故④正确).
由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小;
即当DF⊥AC时,DE最小,此时DF=![]() BC=4.
BC=4.
∴DE=![]() DF=4
DF=4![]() (故③错误).
(故③错误).
当△CDE面积最大时,由④知,此时△DEF的面积最小.
此时S△CDE=S四边形CEFD﹣S△DEF=S△AFC﹣S△DEF=16﹣8=8(故⑤正确).
故选:B.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣![]() +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.
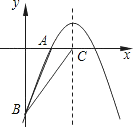
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持亚太地区国家基础设施建设,由中国倡议设立亚投行,截止2015年4月15日,亚投行意向创始成员国确定为57个,其中意向创始成员国数亚洲是欧洲的2倍少2个,其余洲共5个,求亚洲和欧洲的意向创始成员国各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,南沙区政府决定对区直属机关300户家庭的用水情况作一次调查,区政府调查小组随机抽查了其中50户家庭一年的月平均用水量(单位:吨),调查中发现每户用水量均在10﹣14吨/月范围,并将调查结果制成了如图所示的条形统计图.

(1)请将条形统计图补充完整;
(2)这50户家庭月用水量的平均数是 ,众数是 ,中位数是 ;
(3)根据样本数据,估计南沙区直属机关300户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com