
 ),以AB为边在x轴上方作正方形ABCD,点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点,连接AE与BC相交于点F.
),以AB为边在x轴上方作正方形ABCD,点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点,连接AE与BC相交于点F.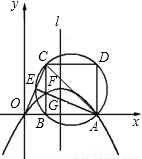
 ,根据三角形内角平分线判定定理,可得出AF是∠CAB的角平分线,如果存在P点,那么P必为抛物线与直线AC的交点,可联立两个函数的解析式求出交点坐标即可.
,根据三角形内角平分线判定定理,可得出AF是∠CAB的角平分线,如果存在P点,那么P必为抛物线与直线AC的交点,可联立两个函数的解析式求出交点坐标即可. ,
, x2-
x2-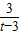 x.
x. ,h),由于GC=OG,
,h),由于GC=OG, -t)2+(h-3+t)2=(
-t)2+(h-3+t)2=( )2+h2
)2+h2 .
. ,
, ,
,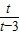 x-
x- .
. 时,
时, =
= ×
× -
- ,
, ,
, ,
,
 x2+
x2+ x.
x. =
= (3
(3 -3),CF=3-2t=3
-3),CF=3-2t=3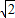 -3.
-3. =
=
 ,
, ,
, ,
, ,
,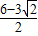 ).
).

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:2004年全国中考数学试题汇编《反比例函数》(03)(解析版) 题型:解答题
 (k<0)的图象经过点A(-
(k<0)的图象经过点A(- ,m),过A作AB⊥x轴于点B,△AOB的面积为
,m),过A作AB⊥x轴于点B,△AOB的面积为 .?
.?
查看答案和解析>>
科目:初中数学 来源:2004年江苏省扬州市中考数学试卷(解析版) 题型:解答题
 ),以AB为边在x轴上方作正方形ABCD,点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点,连接AE与BC相交于点F.
),以AB为边在x轴上方作正方形ABCD,点E是直线OC与正方形ABCD的外接圆除点C以外的另一个交点,连接AE与BC相交于点F.
查看答案和解析>>
科目:初中数学 来源:2004年江苏省扬州市中考数学试卷(解析版) 题型:解答题
 (k<0)的图象经过点A(-
(k<0)的图象经过点A(- ,m),过A作AB⊥x轴于点B,△AOB的面积为
,m),过A作AB⊥x轴于点B,△AOB的面积为 .?
.?
查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《图形的对称》(01)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com