
分析 (1)首先把每个二次根式化为最简二次根式,然后把被开数相同的二次根式进行合并即可;
(2)首先利用括号里的每一项除以$\sqrt{3}$,然后化为最简二次根式,再把被开数相同的二次根式进行合并即可;
(3)利用平方差公式进行计算即可.
解答 解:(1)原式=4$\sqrt{3}$-2$\sqrt{3}$+12$\sqrt{3}$-2$\sqrt{2}$=14$\sqrt{3}$-2$\sqrt{2}$;
(2)原式=5$\sqrt{48÷3}$-6$\sqrt{27÷3}$+4$\sqrt{15÷3}$,
=20-18+4$\sqrt{5}$,
=2+4$\sqrt{5}$;
(3)原式=(2$\sqrt{3}$)2-($\sqrt{6}$)2=12-6=6.
点评 此题主要考查了二次根式的计算,关键是掌握二次根式的混合运算应注意以下几点:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式“,多个不同类的二次根式的和可以看作“多项式“.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 3x2-2x2+1 | B. | $\frac{5}{2}$xy4 | C. | $\frac{3bc}{a}$ | D. | $\frac{a}{2}$-b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
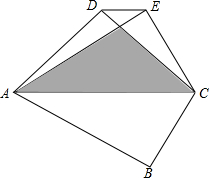 如图,由一副三角板组成的四边形ABCD中,∠B=∠ADC=90°,∠BAC=30°,把△ABC沿AC折叠,点B落在点E处,若两个三角形重叠部分的面积为2$\sqrt{3}$+2,则DE=$\sqrt{2}$.
如图,由一副三角板组成的四边形ABCD中,∠B=∠ADC=90°,∠BAC=30°,把△ABC沿AC折叠,点B落在点E处,若两个三角形重叠部分的面积为2$\sqrt{3}$+2,则DE=$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠EBC=32°,∠AEB=70°.
如图,△ABC中,AD⊥BC于点D,BE平分∠ABC,若∠EBC=32°,∠AEB=70°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com