
�ڵ�����ABC�У�
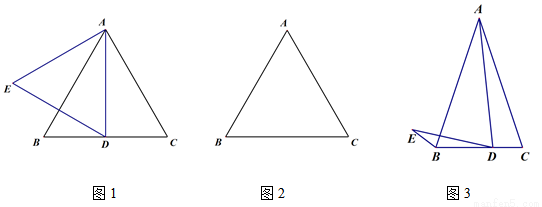
��1����ͼ1������ABCΪ�ȱ������Σ�DΪ�߶�BC�е㣬�߶�AD����ֱ��AB�ĶԳ��߶�Ϊ�߶�AE������DE�����BDE�Ķ���Ϊ___________��
��2������ABCΪ�ȱ������Σ���DΪ�߶�BC��һ���㣨����B��C�غϣ�������AD�����߶�AD�Ƶ�D��ʱ����ת60��õ��߶�DE������BE.
�ٸ���������ͼ2�в�ȫͼ�Σ�
��С��ͨ���۲졢��֤������²⣺�ڵ�D�˶��Ĺ����У�����CD=BE.������ͬѧ�ǵij�����ۣ��γ��˼���֤����˼·��
˼·1��Ҫ֤��CD=BE��ֻ��Ҫ����AE����֤����ADC�ա�AEB��
˼·2��Ҫ֤��CD=BE��ֻ��Ҫ����D��DF��AB����AC��F��֤����ADF�ա�DEB��
˼·3��Ҫ֤��CD=BE��ֻ��Ҫ�ӳ�CB����G��ʹ��BG=CD��֤����ADC�ա�DEG��
����
��ο�����˼·������С��֤��CD=BE.��ֻ��Ҫ��һ�ַ���֤�����ɣ�
��3��С��ķ���������С������ͼ3����AB=AC=kBC��AD=kDE���ҡ�ADE=��C����ʱС������BE��BD��AC����֮������һ���ĵ�������ϵ�����������ϵ��______________________.��ֱ�Ӹ�����������֤����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�챱���ж��������꼶5���ۺ���ϰ��һģ����ѧ�Ծ��������棩 ���ͣ������
�ڵ�����ABC�У�
��1����ͼ1������ABCΪ�ȱ������Σ�DΪ�߶�BC�е㣬�߶�AD����ֱ��AB�ĶԳ��߶�Ϊ�߶�AE������DE�����BDE�Ķ���Ϊ___________��
��2������ABCΪ�ȱ������Σ���DΪ�߶�BC��һ���㣨����B��C�غϣ�������AD�����߶�AD�Ƶ�D��ʱ����ת60��õ��߶�DE������BE.
�ٸ���������ͼ2�в�ȫͼ�Σ�
��С��ͨ���۲졢��֤������²⣺�ڵ�D�˶��Ĺ����У�����CD=BE.������ͬѧ�ǵij�����ۣ��γ��˼���֤����˼·��
˼·1��Ҫ֤��CD=BE��ֻ��Ҫ����AE����֤����ADC�ա�AEB��
˼·2��Ҫ֤��CD=BE��ֻ��Ҫ����D��DF��AB����AC��F��֤����ADF�ա�DEB��
˼·3��Ҫ֤��CD=BE��ֻ��Ҫ�ӳ�CB����G��ʹ��BG=CD��֤����ADC�ա�DEG��
����
��ο�����˼·������С��֤��CD=BE.��ֻ��Ҫ��һ�ַ���֤�����ɣ�
��3��С��ķ���������С������ͼ3����AB=AC=kBC��AD=kDE���ҡ�ADE=��C����ʱС������BE��BD��AC����֮������һ���ĵ�������ϵ�����������ϵ��______________________.��ֱ�Ӹ�����������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�챱���ж��������꼶5���ۺ���ϰ��һģ����ѧ�Ծ��������棩 ���ͣ������
�ֽ���ʽ��  =______________
=______________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�챱���ж��������꼶5���ۺ���ϰ��һģ����ѧ�Ծ��������棩 ���ͣ���ѡ��
ij�������˶��İ��������ֻ�������¼��ij���£�30�죩ÿ�콡���ߵIJ�������λ����������¼������Ƴ�����ͼ��ʾ��ͳ��ͼ����ÿ�����ߵIJ������������У���������λ���ֱ��ǣ� ��

A. 1.2��1.3 B. 1.3��1.3 C. 1.4��1.35 D. 1.4��1.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�챱���ж��������꼶5���ۺ���ϰ��һģ����ѧ�Ծ��������棩 ���ͣ������
��ͼ���ı���ABCDΪƽ���ı��Σ���BAD�Ľ�ƽ����AF��CD�ڵ�E����BC���ӳ����ڵ�F��
��1����֤��BF=CD��
��2������BE����BE��AF����BFA=60�㣬BE=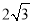 ����ƽ���ı���ABCD���ܳ���
����ƽ���ı���ABCD���ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�챱���ж��������꼶5���ۺ���ϰ��һģ����ѧ�Ծ��������棩 ���ͣ������
�����ǡ�����֪�߶�Ϊֱ����Բ���ij߹���ͼ����.
��֪���߶�AB.
��������ABΪֱ���ġ�O. 
��������ͼ��
��1���ֱ���A��BΪԲ�ģ����� AB�ij�Ϊ�뾶
AB�ij�Ϊ�뾶
�����������ཻ�ڵ�C��D��
��2����ֱ��CD��AB�ڵ�O��
��3����OΪԲ�ģ�OA��Ϊ�뾶��Բ.
���O����������.
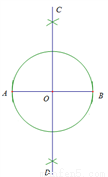
��ش𣺸���ͼ��������_______________________________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ʡ��������Ұ�ذ��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��ͼ��ʾ��P(a,3)��ֱ��y=x+5�ϵ�һ�㣬ֱ�� y=k1x+b��˫����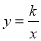 �ཻ��P��Q��1��m��.
�ཻ��P��Q��1��m��.
��1����˫���ߵĽ���ʽ��ֱ��PQ�Ľ���ʽ��
��2������ͼ��ֱ��д������ʽ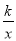 ��k1x+b�Ľ⼯��
��k1x+b�Ľ⼯��
��3����ֱ��y=x+5��x�ύ��A,ֱ��y=k1x+b��x�ύ��M���APQ�����
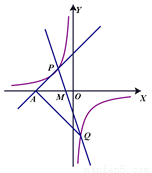
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ɽ��ʡ�������п������ѧ�Ծ��������棩 ���ͣ���ѡ��
��y=kx��4�ĺ���ֵy��x���������С����k��ֵ���������еģ�������
A. ��4 B. 0 C. 1 D. 3
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com