
【题目】△ABC中,BC=12,高AD=8,矩形EFGH的一边GH在BC上,顶点E、F分别在AB、AC上,AD与EF交于点M.
(1)求证:![]() ;
;
(2)设EF=x,EH=y,写出y与x之间的函数表达式;
(3)设矩形EFGH的面积为S,求S与x之间的函数表达式,并写出S的最大值.

【答案】(1)见解析;(2)y=8﹣![]() x(0<x<12);(3)S矩形EFGH=﹣
x(0<x<12);(3)S矩形EFGH=﹣![]() (x﹣6)2+24,Smax=24.
(x﹣6)2+24,Smax=24.
【解析】
(1)先判断出AM是△AEF的高,再判断出△AEF∽△ABC,即可得出结论;(2)先判断出四边形EMDG是矩形,得出DM=EH,进而表示出AM=8﹣y,借助(1)的结论即可得出结论;(3)由矩形的面积公式得出函数关系式,即可得出结论.
解:(1)∵四边形EFGH是矩形,
∴EF∥BC,
∵AD是△ABC的高,
∴AD⊥BC,
∴AM⊥EF,
∵EF∥BC,
∴△AEF∽△ABC,
∴![]() (相似三角形的对应边上高的比等于相似比);
(相似三角形的对应边上高的比等于相似比);
(2)∵四边形EFGH是矩形,
∴∠FEH=∠EHG=90°,
∵AD⊥BC,
∴∠HDM=90°=∠FEH=∠EHG,
∴四边形EMDH是矩形,
∴DM=EH,
∵EF=x,EH=y,AD=8,
∴AM=AD﹣DM=AD﹣EH=8﹣y,
由(1)知,![]() ,
,
∴![]() ,
,
∴y=8﹣![]() x(0<x<12);
x(0<x<12);
(3)由(2)知,y=8﹣![]() x,
x,
∴S=S矩形EFGH=xy=x(8﹣![]() x)=﹣
x)=﹣![]() (x﹣6)2+24,
(x﹣6)2+24,
∵a=﹣![]() <0,
<0,
∴当x=6时,Smax=24.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线C1:y=a(x+1)2﹣4的顶点为C,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
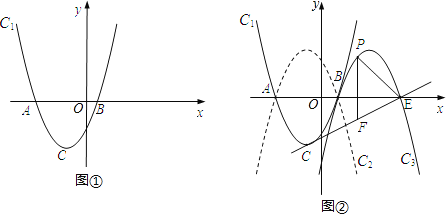
(1)求点C的坐标及a 的值;
(2)如图②,抛物线C2与C1关于x轴对称,将抛物线C2向右平移4个单位,得到抛物线C3.C3与x轴交于点B、E,点P是直线CE上方抛物线C3上的一个动点,过点P作y轴的平行线,交CE于点F.
①求线段PF长的最大值;
②若PE=EF,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足广大手机用户的需求,某移动通信公司推出了三种套餐,资费标准如下表所示:
套餐资费标准 | |||||||
月套餐类型 | 套餐费用 | 套餐包含内容 | 超出套餐后的费用 | ||||
本地主叫市话 | 短信 | 国内移动数据流量 | 本地主叫市话 | 短信 | 国内移动数据流量 | ||
套餐一 | 18元 | 30分钟 | 100条 | 50兆 | 0.1元/ | 0.1元/条 | 0.5元/兆 |
套餐二 | 28元 | 50分钟 | 150条 | 100兆 | |||
套餐三 | 38元 | 80分钟 | 200条 | 200兆 | |||
小莹选择了该移动公司的一种套餐,下面两个统计图都反映了她的手机消费情况.
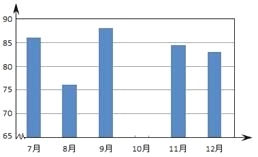
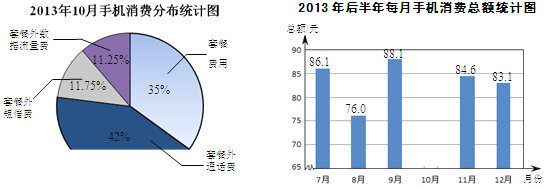
(1)已知小莹2013年10月套餐外通话费为33.6元,则她选择的上网套餐为________套餐(填“一”、“二”或“三”);
(2)补全条形统计图,并在图中标明相应的数据;
(3)根据2013年后半年每月的消费情况,小莹估计自己每月本地主叫市话通话大约430分钟,发短信大约240条,国内移动数据流量使用量大约为120兆,除此之外不再产生其他费用,则小莹应该选择________套餐最划算(填“一”、“二”或“三”);选择该套餐后,她每月的手机消费总额约为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜每千克售价![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=8,DE=5,求BC的长.
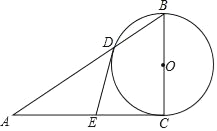
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
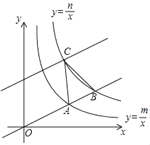
【题目】如图,直线y=![]() x分别与双曲线y=
x分别与双曲线y=![]() (m>0,x>0),双曲线y=
(m>0,x>0),双曲线y=![]() (n>0,x>0)交于点A和点B,且
(n>0,x>0)交于点A和点B,且![]() ,将直线y=
,将直线y=![]() x向左平移6个单位长度后,与双曲线y=
x向左平移6个单位长度后,与双曲线y=![]() 交于点C,若S△ABC=4,则
交于点C,若S△ABC=4,则![]() 的值为_____,mn的值为_____.
的值为_____,mn的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com