
£Ø2013ÄźÕć½ŅåĪŚ12·Ö£©ČēĶ¼1£¬ŅŃÖŖ £Øx£¾
£Øx£¾ £©Ķ¼ĻóÉĻŅ»µćP£¬PA”ĶxÖįÓŚµćA£Øa£¬0£©£¬µćB×ų±źĪŖ£Ø0£¬b£©£Øb£¾0£©£¬¶ÆµćMŹĒyÖįÕż°ėÖįÉĻBµćÉĻ·½µÄµć£¬¶ÆµćNŌŚÉäĻßAPÉĻ£¬¹żµćB×÷ABµÄ“¹Ļߣ¬½»ÉäĻßAPÓŚµćD£¬½»Ö±ĻßMNÓŚµćQ£¬Į¬½įAQ£¬Č”AQµÄÖŠµćĪŖC£®
£©Ķ¼ĻóÉĻŅ»µćP£¬PA”ĶxÖįÓŚµćA£Øa£¬0£©£¬µćB×ų±źĪŖ£Ø0£¬b£©£Øb£¾0£©£¬¶ÆµćMŹĒyÖįÕż°ėÖįÉĻBµćÉĻ·½µÄµć£¬¶ÆµćNŌŚÉäĻßAPÉĻ£¬¹żµćB×÷ABµÄ“¹Ļߣ¬½»ÉäĻßAPÓŚµćD£¬½»Ö±ĻßMNÓŚµćQ£¬Į¬½įAQ£¬Č”AQµÄÖŠµćĪŖC£®
£Ø1£©ČēĶ¼2£¬Į¬½įBP£¬Ēó”÷PABµÄĆ껿£»
£Ø2£©µ±µćQŌŚĻ߶ĪBDÉĻŹ±£¬ČōĖıߊĪBQNCŹĒĮāŠĪ£¬Ć껿ĪŖ £¬Ēó“ĖŹ±PµćµÄ×ų±ź£»
£¬Ēó“ĖŹ±PµćµÄ×ų±ź£»
£Ø3£©µ±µćQŌŚÉäĻßBDÉĻŹ±£¬ĒŅa=3£¬b=1£¬ČōŅŌµćB£¬C£¬N£¬QĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£¬ĒóÕāøöĘ½ŠŠĖıߊĪµÄÖܳ¤£®
½ā£ŗ£Ø1£©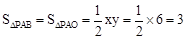 ”£
ӣ
£Ø2£©ČēĶ¼1£¬”ßĖıߊĪBQNCŹĒĮāŠĪ£¬
”ąBQ=BC=NQ£¬”ĻBQC=”ĻNQC”£
”ßAB”ĶBQ£¬CŹĒAQµÄÖŠµć£¬”ąBC=CQ=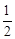 AQ”£”ą”ĻBQC=60”ć£¬”ĻBAQ=30”ć”£
AQ”£”ą”ĻBQC=60”ć£¬”ĻBAQ=30”ć”£
ŌŚ”÷ABQŗĶ”÷ANQÖŠ£¬”ß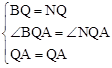 £¬”ą”÷ABQ”Õ”÷ANQ£ØSAS£©”£
£¬”ą”÷ABQ”Õ”÷ANQ£ØSAS£©”£
”ą”ĻBAQ=”ĻNAQ=30”ć”£”ą”ĻBAO=30”ć”£
”ßSĖıߊĪBQNC= £¬”ąBQ=2”£”ąAB=
£¬”ąBQ=2”£”ąAB= BQ=
BQ= ”£”ąOA=
”£”ąOA=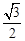 AB=3”£
AB=3ӣ
ÓÖ”ßPµćŌŚ·“±ČĄżŗÆŹż µÄĶ¼ĻóÉĻ£¬”ąPµć×ų±źĪŖ£Ø3£¬2£©”£
µÄĶ¼ĻóÉĻ£¬”ąPµć×ų±źĪŖ£Ø3£¬2£©”£
£Ø3£©”ßOB=1£¬OA=3£¬”ąAB=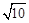 ”£
ӣ
”ß”÷AOB”×”÷DBA£¬”ą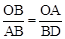 ”£”ąBD=3
”£”ąBD=3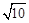 ”£
ӣ
¢ŁČēĶ¼2£¬µ±µćQŌŚĻ߶ĪBDÉĻ£¬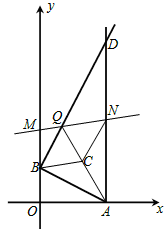
”ßAB”ĶBD£¬CĪŖAQµÄÖŠµć£¬”ąBC=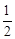 AQ”£
AQӣ
”ßĖıߊĪBNQCŹĒĘ½ŠŠĖıߊĪ£¬”ąQN=BC£¬CN=BQ£¬CN”ĪBD”£
”ą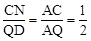 £¬”ąBQ=CN=
£¬”ąBQ=CN=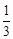 BD=
BD=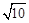 ӣ
ӣ
”ąAQ=2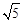 ”£
ӣ
”ąCĖıߊĪBQNC=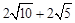 ”£
ӣ
¢ŚČēĶ¼3£¬µ±µćQŌŚĻ߶ĪBDµÄŃÓ³¤ĻßÉĻ£¬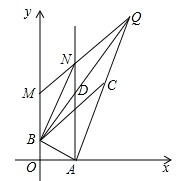
”ßAB”ĶBD£¬CĪŖAQµÄÖŠµć£¬
”ąBC=CQ=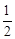 AQ”£
AQӣ
”ąĘ½ŠŠĖıߊĪBNQCŹĒĮāŠĪ£¬BN=CQ£¬BN”ĪCQ”£
”ą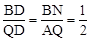 ”£”ąBQ=3BD=9
”£”ąBQ=3BD=9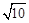 ”£
ӣ
”ą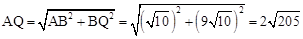 ”£
ӣ
”ąCĖıߊĪBNQC=2AQ= ”£
ӣ
½āĪö


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ĪŅŹŠÄ³Źß²ĖÉś²ś»łµŲŌŚĘųĪĀ½ĻµĶŹ±,ÓĆ×°ÓŠŗćĪĀĻµĶ³µÄ“óÅļŌŌÅąŅ»ÖÖŌŚ×ŌČ»¹āÕÕĒŅĪĀ¶ČĪŖ18”ęµÄĢõ¼žĻĀÉś³¤×īæģµÄŠĀĘ·ÖÖ£®ČēĶ¼ŹĒijĢģŗćĪĀĻµĶ³“ÓæŖĘōµ½¹Ų±Õ¼°¹Ų±Õŗó,“óÅļÄŚĪĀ¶Čy(”ę)Ėꏱ¼äx (Š”Ź±)±ä»ÆµÄŗÆŹżĶ¼Ļó,ĘäÖŠBC¶ĪŹĒĖ«ĒśĻß µÄŅ»²æ·Ö£®Ēėøł¾ŻĶ¼ÖŠŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
µÄŅ»²æ·Ö£®Ēėøł¾ŻĶ¼ÖŠŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ŗćĪĀĻµĶ³ŌŚÕāĢģ±£³Ö“óÅļÄŚĪĀ¶Č18”ęµÄŹ±¼äÓŠ¶ąÉŁŠ”Ź±£æ
£Ø2£©ĒókµÄÖµ£»
£Ø3£©µ±x=16Ź±,“óÅļÄŚµÄĪĀ¶ČŌ¼ĪŖ¶ąÉŁ¶Č£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ŅŃÖŖĖ«ĒśĻß ÉĻŅ»µćM£Ø1£¬m£©ŗĶĖ«ĒśĻß
ÉĻŅ»µćM£Ø1£¬m£©ŗĶĖ«ĒśĻß ÉĻŅ»µćN£Øn£¬3£©.
ÉĻŅ»µćN£Øn£¬3£©.
£Ø1£©Ēóm”¢nµÄÖµ£»
£Ø2£©Ēó”÷OMNµÄĆ껿.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ŅŃÖŖ£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬µćAŌŚxÖįøŗ°ėÖįÉĻ£¬µćBŌŚyÖįÕż°ėÖįÉĻ£¬OA=OB£¬ŗÆŹż µÄĶ¼ĻóÓėĻ߶ĪAB½»ÓŚMµć£¬ĒŅAM=BM£®
µÄĶ¼ĻóÓėĻ߶ĪAB½»ÓŚMµć£¬ĒŅAM=BM£®
£Ø1£©ĒóµćMµÄ×ų±ź£»
£Ø2£©ĒóÖ±ĻßABµÄ½āĪöŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ČēĶ¼£¬Ö±Ļß Óė·“±ČĄżŗÆŹż
Óė·“±ČĄżŗÆŹż µÄĶ¼Ļó½»ÓŚA”¢BĮ½µć£¬ÓėxÖį½»ÓŚµćC£¬ŅŃÖŖµćAµÄ×ų±źĪŖ£Ø£1£¬m£©£®
µÄĶ¼Ļó½»ÓŚA”¢BĮ½µć£¬ÓėxÖį½»ÓŚµćC£¬ŅŃÖŖµćAµÄ×ų±źĪŖ£Ø£1£¬m£©£®
£Ø1£©Ē󷓱ȥżŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ČōµćP£Øn£¬1£©ŹĒ·“±ČĄżŗÆŹżĶ¼ĻóÉĻŅ»µć£¬¹żµćP×÷PE”ĶxÖįÓŚµćE£¬ŃÓ³¤EP½»Ö±ĻßABÓŚµćF£¬Ēó”÷CEFµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ŅŃÖŖ£ŗČēĶ¼£¬Ņ»“ĪŗÆŹżµÄĶ¼ĻóÓėyÖį½»ÓŚC£Ø0£¬3£©£¬ĒŅÓė·“±ČĄżŗÆŹż µÄĶ¼ĻóŌŚµŚŅ»ĻóĻŽÄŚ½»ÓŚA£¬BĮ½µć£¬ĘäÖŠA£Ø1£¬a£©£¬ĒóÕāøöŅ»“ĪŗÆŹżµÄ½āĪöŹ½£®
µÄĶ¼ĻóŌŚµŚŅ»ĻóĻŽÄŚ½»ÓŚA£¬BĮ½µć£¬ĘäÖŠA£Ø1£¬a£©£¬ĒóÕāøöŅ»“ĪŗÆŹżµÄ½āĪöŹ½£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬”÷ABCµÄ±ßACŌŚxÖįÉĻ£¬±ßBC”ĶxÖį£¬Ė«ĒśĻß Óė±ßBC½»ÓŚµćD£Ø4£¬m£©£¬Óė±ßAB½»ÓŚµćE£Ø2£¬n£©£®
Óė±ßBC½»ÓŚµćD£Ø4£¬m£©£¬Óė±ßAB½»ÓŚµćE£Ø2£¬n£©£®
£Ø1£©Ēón¹ŲÓŚmµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©ČōBD=2£¬tan”ĻBAC= £¬ĒókµÄÖµŗĶµćBµÄ×ų±ź£®
£¬ĒókµÄÖµŗĶµćBµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćA£Ø©3£¬4£©¹ŲÓŚyÖįµÄ¶Ō³ĘµćĪŖµćB£¬Į¬½ÓAB£¬·“±ČĄżŗÆŹż £Øx£¾0£©µÄĶ¼Ļó¾¹żµćB£¬¹żµćB×÷BC”ĶxÖįÓŚµćC£¬µćPŹĒøĆ·“±ČĄżŗÆŹżĶ¼ĻóÉĻČĪŅāŅ»µć£¬¹żµćP×÷PD”ĶxÖįÓŚµćD£¬µćQŹĒĻ߶ĪABÉĻČĪŅāŅ»µć£¬Į¬½ÓOQ”¢CQ£®
£Øx£¾0£©µÄĶ¼Ļó¾¹żµćB£¬¹żµćB×÷BC”ĶxÖįÓŚµćC£¬µćPŹĒøĆ·“±ČĄżŗÆŹżĶ¼ĻóÉĻČĪŅāŅ»µć£¬¹żµćP×÷PD”ĶxÖįÓŚµćD£¬µćQŹĒĻ߶ĪABÉĻČĪŅāŅ»µć£¬Į¬½ÓOQ”¢CQ£®
£Ø1£©ĒókµÄÖµ£»
£Ø2£©ÅŠ¶Ļ”÷QOCÓė”÷PODµÄĆ껿ŹĒ·ńĻąµČ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
Ņ»øöÕż·½ĢåµÄĮłøöĆęÉĻ·Ö±š±źÓŠ1”¢2”¢3”¢4”¢5”¢6£¬øł¾ŻĶ¼ÖŠ“Óø÷øö·½Ļņ擵½µÄŹż×Ö£¬½ā“šĻĀĆęµÄĪŹĢā£ŗ
£Ø1£©”°£æ”±“¦µÄŹż×ÖŹĒŹ²Ć“£æ
£Ø2£©ĆæĮ½øöĻą¶ŌĆęÉĻµÄŹż×Ö·Ö±šŹĒŹ²Ć“£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com