
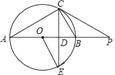
【题目】如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】分析:(1)连结OC,如图,根据圆周角定理得∠POC=2∠CAB,由于∠POE=2∠CAB,则∠POC=∠POE,根据等腰三角形的性质即可得到CE⊥AB;
(2)由CE⊥AB得∠P+∠PCE=90°,加上∠E=∠OCD,∠P=∠E,所以∠OCD+∠PCE=90°,则OC⊥PC,然后根据切线的判定定理即可得到结论.
(3)设⊙O的半径为r,OD=x,则BD=2x,r=3x,易证得Rt△OCD∽Rt△OPC,根据相似三角形的性质得OC2=ODOP,即(3x)2=x(3x+9),解出x,即可得圆的半径;同理可得PC2=PDPO=(PB+BD)(PB+OB)=162,可计算出PC,然后在Rt△OCP中,根据正切的定义即可得到tan∠P的值.
详解:(1)证明:连接OC,
∴∠COB=2∠CAB,
又∠POE=2∠CAB.
∴∠COD=∠EOD,
又∵OC=OE,
∴∠ODC=∠ODE=90°,
即CE⊥AB;
(2)证明:∵CE⊥AB,∠P=∠E,
∴∠P+∠PCD=∠E+∠PCD=90°,
又∠OCD=∠E,
∴∠OCD+∠PCD=∠PCO=90°,
∴PC是⊙O的切线;
(3)解:设⊙O的半径为r,OD=x,则BD=2x,r=3x,
∵CD⊥OP,OC⊥PC,
∴Rt△OCD∽Rt△OPC,
∴OC2=ODOP,即(3x)2=x(3x+9),
解之得x=![]() ,
,
∴⊙O的半径r=![]() ,
,
同理可得PC2=PDPO=(PB+BD)(PB+OB)=162,
∴PC=9![]() ,
,
在Rt△OCP中,tan∠P=![]() .
.


科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
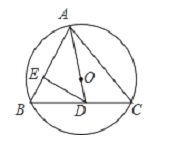
【题目】如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)求证:∠ACB+∠BAD=90°;
(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB.求证:AC=2DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 y=x2+bx+![]() 与 y轴交于点 B,将该抛物线平移,使其经过点 A(-
与 y轴交于点 B,将该抛物线平移,使其经过点 A(-![]() ,0),且与 x轴交于另一点 C.若 b≤﹣2,则线段 OB,OC的大小关系是( )
,0),且与 x轴交于另一点 C.若 b≤﹣2,则线段 OB,OC的大小关系是( )
A. OB≤OC B. OB<OC C. OB≥OC D. OB>OC
查看答案和解析>>
科目:初中数学 来源: 题型:
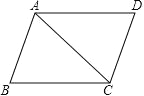
【题目】如图,四边形ABCD 是平行四边形,AB=c,AC=b,BC=a,抛物线 y=ax2+bx﹣c 与 x 轴的一个交点为(m,0).
(1)若四边形ABCD是正方形,求抛物线y=ax2+bx﹣c的对称轴;
(2)若 m=![]() c,ac﹣4b<0,且 a,b,c为整数,求四边形 ABCD的面积.
c,ac﹣4b<0,且 a,b,c为整数,求四边形 ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宾馆有50间房供游客居住,当每间房每天定价为180元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的每间房每天支出 20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价比定价 180元增加 x元,则有( )
A. (x﹣20)(50﹣![]() )=10890 B. x(50﹣
)=10890 B. x(50﹣![]() )﹣50×20=10890
)﹣50×20=10890
C. (180+x﹣20)(50﹣![]() )=10890 D. (x+180)(50﹣
)=10890 D. (x+180)(50﹣![]() )﹣50×20=10890
)﹣50×20=10890
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正方形ABCD,点E,F分别在AB,CD上,DG⊥EF于点 H.
(1)求证:DG=EF;
(2)在图①的基础上连接AH,如图②,若 AH=AD,试确定DF与 CG的数量关系,并说明理由;
(3)在(2)的条件下,作∠FEK=45°,点 K在 BC边上,如图③,若AE=KG=2,求EK的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,cosB=0.6,把这个直角三角形绕顶点C旋转后得到Rt△A'B'C,其中点B'正好落在AB上,A'B'与AC相交于点D,那么B′D:CD=_____.
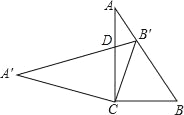
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,
点G是BC、AE延长线的交点,AG与CD相交于点F。
求证:四边形ABCD是正方形;
当AE=2EF时,判断FG与EF有何数量关系?并证明你的结论。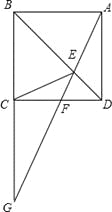
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com