
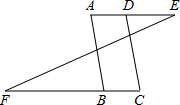
 如图,AD∥BC,∠A=∠C,说明AB∥DC.
如图,AD∥BC,∠A=∠C,说明AB∥DC.  灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
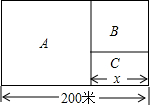 如图,一块长方形地,长为200米,建筑商将它分为A、B、C三个区域,A、B为正方形,现计划A区域建筑住宅区,B区域建筑商场,C区域开辟为公园.若已知C区域的面积为3200m2,设C区域的长为x米,则能列出关于x的方程是( )
如图,一块长方形地,长为200米,建筑商将它分为A、B、C三个区域,A、B为正方形,现计划A区域建筑住宅区,B区域建筑商场,C区域开辟为公园.若已知C区域的面积为3200m2,设C区域的长为x米,则能列出关于x的方程是( )| A. | x2+100x-1600=0 | B. | x2-100x+1600=0 | C. | x2-100x-1600=0 | D. | x2+100x+1600=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
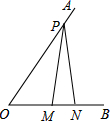 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M、N在边OB上,PM=PN,若MN=2,则△POM的面积为15$\sqrt{3}$.
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M、N在边OB上,PM=PN,若MN=2,则△POM的面积为15$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com