
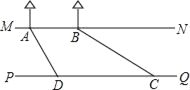
【题目】如图,在城市改造中,市政府欲在一条人工河上架一座桥,河的两岸PQ与MN平行,河岸MN上有A、B两个相距50米的凉亭,小亮在河对岸D处测得∠ADP=60°,然后沿河岸走了110米到达C处,测得∠BCP=30°,求这条河的宽.(结果保留根号)
科目:初中数学 来源: 题型:
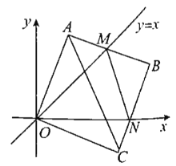
【题目】在正方形方格纸中,我们把顶点都在“格点”上的三角形称为“格点三角形“,如图,△ABC是一个格点三角形,点A的坐标为(﹣1,2).
(1)点B的坐标为 ,△ABC的面积为 ;
(2)在所给的方格纸中,请你以原点O为位似中心,将△ABC放大为原来的2倍,放大后点A、B的对应点分别为A1、B1,点B1在第一象限;
(3)在(2)中,若P(a,b)为线段AC上的任一点,则放大后点P的对应点P1的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东门天虹商场购进一批“童乐”牌玩具,每件成本价30元,每件玩具销售单价x(元)与每天的销售量y(件)的关系如下表:

若每天的销售量y(件)是销售单价x(元)的一次函数
(1)求y与x的函数关系式;
(2)设东门天虹商场销售“童乐”牌儿童玩具每天获得的利润为w(元),当销售单价x为何值时,每天可获得最大利润?此时最大利润是多少?
(3)若东门天虹商场销售“童乐”牌玩具每天获得的利润最多不超过15000元,最低不低于12000元,那么商场该如何确定“童乐”牌玩具的销售单价的波动范围?请你直接给出销售单价x的范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在以点O为原点的平面直角坐标系中,边长为1的正方形OABC的两顶点A,C分别在y轴,![]() 轴的正半轴上,现将正方形OABC绕点О顺时针旋转,当点A第一次落在直线
轴的正半轴上,现将正方形OABC绕点О顺时针旋转,当点A第一次落在直线![]() 上时,停止转动,旋转过程中,AB边交直线
上时,停止转动,旋转过程中,AB边交直线![]() 于点M,BC边交轴于点N.
于点M,BC边交轴于点N.
(1)旋转停止时正方形旋转的度数是_________.
(2)在旋转过程中,当MN和AC平行时,
①![]() 与
与![]() 是否全等?此时正方形OABC旋转的度数是多少?
是否全等?此时正方形OABC旋转的度数是多少?
②直接写出![]() 的周长的值,并判断这个值在正方形OABC的旋转过程中是否发生变化.
的周长的值,并判断这个值在正方形OABC的旋转过程中是否发生变化.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
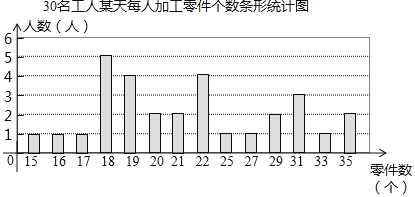
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC 有一外接圆,其中∠B=90°,AB>BC,今欲在![]() 上找一点 P, 使得
上找一点 P, 使得![]() ,下是甲、乙两人的作法:
,下是甲、乙两人的作法:
甲:①取 AB 的中点 D:②过点 D 作直线 AC 的平行线,交![]() 于点 P,则点 P 即为所求,
于点 P,则点 P 即为所求,
乙:①取 AC 的中点 E;②过点 E 作直线AB 的平行线,交![]() 于点 P,则点 P 即为所求,
于点 P,则点 P 即为所求,
对于甲、乙两人的作法,下列判断正确的是( )
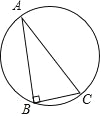
A. 两人皆正确 B. 两人皆错误 C. 甲正确,乙错误 D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
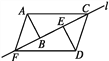
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决下列两个问题:
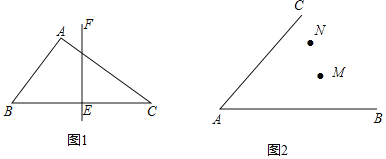
(1)如图1,在△ABC中,AB=3,AC=4,BC=5.EF垂直且平分BC.点P在直线EF上,直接写出PA+PB的最小值,并在图中标出当PA+PB取最小值时点P的位置;
解:PA+PB的最小值为 .
(2)如图2.点M、N在∠BAC的内部,请在∠BAC的内部求作一点P,使得点P到∠BAC两边的距离相等,且使PM=PN.(尺规作图,保留作图痕迹,无需证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com