
【题目】在数轴上,点A,B,C表示的数分别是-6,10,12.点A以每秒3个单位长度的速度向右运动,同时线段BC以每秒1个单位长度的速度也向右运动.
(1)运动前线段AB的长度为________;
(2)当运动时间为多长时,点A和线段BC的中点重合?
(3)试探究是否存在运动到某一时刻,线段AB=![]() AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
AC?若存在,求出所有符合条件的点A表示的数;若不存在,请说明理由.
【答案】(1)16;(2)![]() ;(3)15或19.
;(3)15或19.
【解析】
(1)根据两点间的距离公式即可求解;
(2)先根据中点坐标公式求得B、C的中点,再设当运动时间为x秒长时,点A和线段BC的中点重合,根据路程差的等量关系列出方程求解即可;
(3)设运动时间为y秒,分两种情况:①当点A在点B的左侧时,②当点A在线段AC上时,列出方程求解即可.
(1)运动前线段AB的长度为10﹣(﹣6)=16;
(2)设当运动时间为x秒长时,点A和线段BC的中点重合,依题意有
﹣6+3t=11+t,
解得t= ![]()
故当运动时间为 ![]() 秒长时,点A和线段BC的中点重合
秒长时,点A和线段BC的中点重合
(3)存在,理由如下:设运动时间为y秒,
①当点A在点B的左侧时,依题意有(10+y)﹣(3y﹣6)=2,解得y=7,
﹣6+3×7=15;
②当点A在线段BC上时,依题意有(3y-6)-(10+y)= ![]()
解得y= ![]()
![]()
综上所述,符合条件的点A表示的数为15或19.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
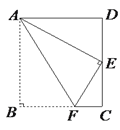
【题目】如图,四边形ABCD为矩形纸片,把纸片ABCD折叠,使点B恰好落在CD边的中点E处, 折痕为AF,若CD=6,则AF等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
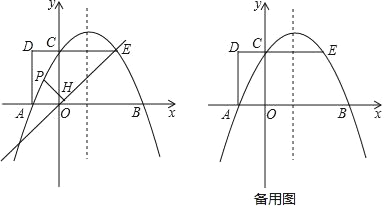
【题目】如图1,抛物线y=ax2+bx+2 与x轴交于A,B两点,与y轴交于点C,AB=4.矩形OADC的边CD=1,延长DC交抛物线于点E.
(1)求抛物线的表达式;
(2)点P是直线EO 上方抛物线上的一个动点,作PH⊥EO,垂足为H,求PH的最大值;
(3)点M在抛物线上,点N在抛物线的对称轴上,若四边形ACMN是平行四边形,求点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要印制商品宣传材料,甲印刷厂的收费标准是:每份材料收1元印制费,另收1 500元制版费;乙印刷厂的收费标准是:每份材料收2.5元印制费,不收制版费.
(1)分别写出两厂的收费y(元)与印制数量x(份)之间的关系式;
(2)在同一直角坐标系中画出它们的图象;
(3)根据图象回答下列问题:印制800份宣传材料时,选择哪一家印刷厂比较合算?商场计划花费3 000元用于印刷上述宣传材料,找哪一家印刷厂印制宣传材料多一些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )

A. 3 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
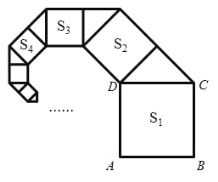
【题目】如图,正方形 ABCD 的边长为1,其面积为 S1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为 S2,…,按此规律继续下去,则 S9的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
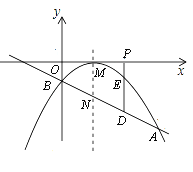
【题目】已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,-4),B点在y轴上.
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,-4),B点在y轴上.
(1)求m的值及这个二次函数的解析式;
(2)在x轴上找一点Q,使△QAB的周长最小,并求出此时Q点坐标;
(3)若P(t,0)是x轴上的一个动点,过P作x轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①设线段DE的长为h,当0<t<3时,求h与t之间的函数关系式;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com