
【题目】已知:⊙O的直径为3,线段AC=4,直线AC和PM分别与⊙O相切于点A,M.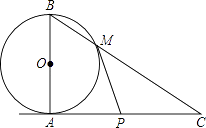
(1)求证:点P是线段AC的中点;
(2)求sin∠PMC的值.
【答案】
(1)
证明:连结OM,如图,
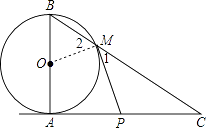
∵直线AC和PM分别与⊙O相切于点A,M,
∴PM=PA,OM⊥MP,BA⊥AC,
∴∠OMP=90°,∠BAC=90°,
∴∠1+∠2=90°,∠B+∠C=90°,
而∠2=∠B,
∴∠1=∠C,
∴PC=PM,
∴PA=PC,
∴点P是线段AC的中点;
(2)
解:由(1)∠PMC=∠C,
在Rt△ABC中,AB=3,AC=4,
∴BC= ![]() =5,
=5,
∴sin∠C= ![]() =
= ![]() ,
,
即sin∠PMC= ![]() .
.
【解析】(1)连结OM,根据切线的性质得OM⊥MP,BA⊥AC,根据切线长定理得PM=PA,则∠1+∠2=90°,∠B+∠C=90°,而∠2=∠B,所以∠1=∠C,于是得到PC=PM,则PA=PC;(2)由于∠PMC=∠C,在Rt△ABC中,先根据勾股定理计算出BC=5,然后根据正弦的定义得到sin∠C= ![]() =
= ![]() ,于是得到sin∠PMC的值.
,于是得到sin∠PMC的值.
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8,BC=10,以B为圆心,任意长为半径画弧分别交BA、BC于点M和N,再分别以M、N为圆心,大于 ![]() MN长为半径画弧,两弧交于点P,连结BP并延长交AC于点D,若△BDC的面积为20,则△ABD的面积为( )
MN长为半径画弧,两弧交于点P,连结BP并延长交AC于点D,若△BDC的面积为20,则△ABD的面积为( ) 
A.20
B.18
C.16
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级为建立学习兴趣小组,对语文、数学、英语、物理、化学、思想品德、历史、综合共八个科目的喜欢情况进行问卷调查(每人只选一项),下表是随机抽取部分学生的问卷进行统计的结果:
科目 | 语文 | 数学 | 英语 | 物理 | 化学 | 思想品德 | 历史 | 综合 |
人数 | 6 | 10 | 11 | 12 | 10 | 9 | 8 | 14 |

根据表中信息,解答下列问题:
(1)本次随机抽查的学生共有人;
(2)本次随机抽查的学生中,喜欢科目的人数最多;
(3)根据上表中的数据补全条形统计图;
(4)如果该校九年级有600名学生,那么估计该校九年级喜欢综合科目的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知边长为4的正方形ABCD,P是BC边上一动点(与B、C不重合),连结AP,作PE⊥AP交∠BCD的外角平分线于E.设BP=x,△PCE面积为y,则y与x的函数关系式是( )
A.y=2x+1
B.y= ![]() x﹣2x2
x﹣2x2
C.y=2x﹣ ![]() x2
x2
D.y=2x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的边AC在x轴上,边BC⊥x轴,双曲线y= ![]() 与边BC交于点D(4,m),与边AB交于点E(2,n).
与边BC交于点D(4,m),与边AB交于点E(2,n).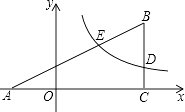
(1)求n关于m的函数关系式;
(2)若BD=2,tan∠BAC= ![]() ,求k的值和点B的坐标.
,求k的值和点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )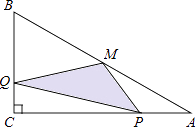
A.一直增大
B.一直减小
C.先减小后增大
D.先增大后减少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com