
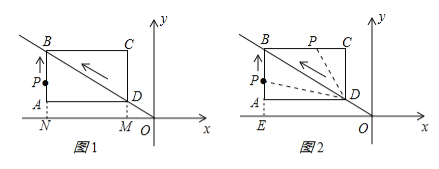
����Ŀ����ͼ1������ABCD�����������������ϣ���D������ԭ��O�غϣ���AD=8��AB=6����ͼ2������ABCD��OB������ÿ��1����λ���ȵ��ٶ��˶���ͬʱ��P��A�����Ҳ��ÿ��1����λ���ȵ��ٶ��ؾ���ABCD�ı�AB������B���C�˶�������P�����Cʱ������ABCD�͵�Pͬʱֹͣ�˶������P���˶�ʱ��Ϊt�룮

��1����t=5ʱ����ֱ��д����D����P�����ꣻ
��2������P���߶�AB���߶�BC���˶�ʱ�������PBD�����S����t�ĺ�����ϵʽ����д����Ӧt��ȡֵ��Χ��
��3����P���߶�AB���߶�BC���˶�ʱ����PE��x�ᣬ����Ϊ��E������PEO����BCD����ʱ�������Ӧ��tֵ��
���𰸡���1��D����4��3����P����12��8������2��![]() ����3��6��
����3��6��
��������
�����������1���ӳ�CD��x����M���ӳ�BA��x����N����CM��x�ᣬBN��x�ᣬAD��x�ᣬBN��DM���ɾ��ε����ʵó����ɶ������BD��BO=15����ƽ���ߵó���ABD�ס�NBO���ó�����ʽ![]() �����BN��NO���ó�OM��DN��PN�����ɵó���D��P�����ꣻ
�����BN��NO���ó�OM��DN��PN�����ɵó���D��P�����ꣻ
��2������P�ڱ�AB��ʱ��BP=6��t���������ε������ʽ�ó�S=![]() BPAD��������P�ڱ�BC��ʱ��BP=t��6��ͬ���ó�S=
BPAD��������P�ڱ�BC��ʱ��BP=t��6��ͬ���ó�S=![]() BPAB�����ɵó������
BPAB�����ɵó������
��3�����D��![]() ��
��![]() ���������������������P�ڱ�AB��ʱ��P��
���������������������P�ڱ�AB��ʱ��P��![]() ��
��![]() ������
������![]() ��
��![]() ʱ���ֱ����t��ֵ��
ʱ���ֱ����t��ֵ��
������P�ڱ�BC��ʱ��P��![]() ��
��![]() ������
������![]() ��
��![]() ʱ���ֱ����t��ֵ���ɣ�
ʱ���ֱ����t��ֵ���ɣ�
�����������1���ӳ�CD��x����M���ӳ�BA��x����N����ͼ1��ʾ����CM��x�ᣬBN��x�ᣬAD��x�ᣬBN��DM�����ı���ABCD�Ǿ��Σ����BAD=90�㣬CD=AB=6��BC=AD=8����BD=![]() =10����t=5ʱ��OD=5����BO=15����AD��NO�����ABD�ס�NBO����
=10����t=5ʱ��OD=5����BO=15����AD��NO�����ABD�ס�NBO����![]() ����
����![]() ����BN=9��NO=12����OM=12��8=4��DM=9��6=3��PN=9��1=8����D����4��3����P����12��8����
����BN=9��NO=12����OM=12��8=4��DM=9��6=3��PN=9��1=8����D����4��3����P����12��8����
��2����ͼ2��ʾ������P�ڱ�AB��ʱ��BP=6��t����S=![]() BPAD=
BPAD=![]() ��6��t����8=��4t+24��
��6��t����8=��4t+24��
������P�ڱ�BC��ʱ��BP=t��6����S=![]() BPAB=
BPAB=![]() ��t��6����6=3t��18��
��t��6����6=3t��18��
����������![]() ��
��
��3����� D��![]() ��
��![]() ����
����
������P�ڱ�AB��ʱ��P��![]() ��
��![]() ������
������![]() ʱ��
ʱ��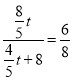 ����ã�t=6��
����ã�t=6��
��![]() ʱ��
ʱ��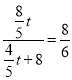 ����ã�t=20���������⣬��ȥ����
����ã�t=20���������⣬��ȥ����
������P�ڱ�BC��ʱ��P��![]() ��
��![]() ������
������![]() ʱ��
ʱ��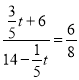 ����ã�t=6��
����ã�t=6��
��![]() ʱ��
ʱ��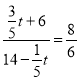 ����ã�
����ã�![]() ���������⣬��ȥ����
���������⣬��ȥ����
������������t=6ʱ����PEO����BCD���ƣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ� �������Կ���4ҳ�α���
A.������������������ͳ������
B.��������������ͳ��������
C.��ȿ�������������Ҳ�����Ǹ�����
D.���еķ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
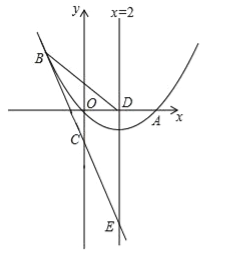
����Ŀ����ͼ����֪�����߾���ԭ��o��x����һ��A��4��0���������߶���ΪE�����ĶԳ�����x�ύ�ڵ�D��ֱ��y=��2x��1������������һ��B����2��m������y�ύ�ڵ�C���������ߵĶԳ��ύ�ڵ�F��
��1����m��ֵ���������߶�Ӧ�Ľ���ʽ��
��2��P��x��y�����������ϵ�һ�㣬��S��ADP=S��ADC��������з��������ĵ�P�����ꣻ
��3����Q��ƽ��������һ�㣬��M�ӵ�F�������ضԳ���������ÿ��1����λ���ȵ��ٶ������˶������M���˶�ʱ��Ϊt�룬�Ƿ���ʹ��Q��A��E��M�ĵ�Ϊ������ı��������Σ����ܣ���ֱ��д����M���˶�ʱ��t��ֵ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��50��ѧ����һ�ΰ�ȫ֪ʶ�����ɼ�������Ϊ10�����ֲ������ʾ��
�ɼ������� | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
�������ˣ� | 0 | 0 | 0 | 1 | 0 | 1 | 3 | 5 | 6 | 19 | 15 |
��ΰ�ȫ֪ʶ�����ɼ����������� ��
A. 5�� B. 6�� C. 9�� D. 10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��x2����ƽ��2����λ���ȣ�������ƽ��3����λ���Ⱥõ��������ߵĽ���ʽΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
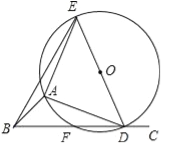
����Ŀ����ͼ����ABC=45�㣬��ADE�ǵ���ֱ�������Σ�AE=AD������A��D�ֱ�����ABC������BA��BC�ϻ����������B�غϣ�����ADE�����Բ��BC�ڵ�F��OΪԲ�ģ�
��1��ֱ��д����AFE�Ķ�����
��2������D�ڵ�F���Ҳ�ʱ������֤��EF��DF=![]() AF��
AF��
����AB=![]() ��
��![]() ��BE��
��BE��![]() ������O�����S��ȡֵ��Χ��
������O�����S��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ե�AΪ����������Rt��ABC������Rt��ADE�����С�BAC=��DAE=90�㣬��ͼ1��ʾ���ã�ʹ��һֱ�DZ��غϣ�����BD��CE��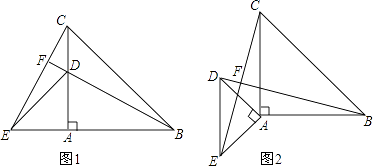
��1�����ж�BD��CE��������ϵ����˵�����ɣ�
��2���ӳ�BD��CE�ڵ�F�������BFC�Ķ�����
��3������������ֱ�������ΰ���ͼ2���ã���1���еĽ����Ƿ��Գ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD��GE��AQƽ�֡�FAC����BD��Q,��GFA=50�㣬��Q=25�㣬���ACB�Ķ���( )
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com