
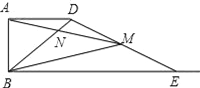
【题目】如图,已知AB=2,AD=4,∠DAB=90°,AD∥BC.E是射线BC上的动点(点E与点B不重合),M是线段DE的中点,连结BD,交线段AM于点N,如果以A,N,D为顶点的三角形与△BME相似,则线段BE的长为___________.
【答案】8或2
【解析】试题分析:因为如果三角形ADN和BME相似,一定不相等的角是∠ADN和∠MBE,因为AD∥BC,如果两角相等,那么M与D重合,显然不合题意,故应分两种情况进行讨论,设BE长为x.
①如图1,当∠ADN=∠BEM时,那么∠ADB=∠BEM,作DF⊥BE,垂足为F,tan∠ADB=tan∠BEM,AB:AD=DF:FE=AB:(BE﹣AD).即2:4=2:(x﹣4).解得x=8.即BE=8.
②如图2,当∠ADB=∠BME,而∠ADB=∠DBE,∴∠DBE=∠BME,∵∠E是公共角,
∴△BED∽△MEB,∴![]() ,BE2=DEEM=
,BE2=DEEM=![]() DE2=
DE2=![]() (DF2+EF2),
(DF2+EF2),
∴BE2=![]() [22+(4﹣x)2],∴x1=2,x2=﹣10(舍去),∴BE=2.
[22+(4﹣x)2],∴x1=2,x2=﹣10(舍去),∴BE=2.
综上所述线段BE为8或2,
故答案为8或2.




 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为10 cm,点E,F,G,H分别从点A,B,C,D出发,以2 cm/s的速度同时分别向点B,C,D,A运动.
(1)在运动的过程中,四边形EFGH是何种四边形?请说明理由.
(2)运动多少秒后,四边形EFGH的面积为52cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,BE为∠ABC的角平分线交AC于E,交AD于F,FG∥BD,交AC于G,过E作EH⊥CD于H,连接FH,下列结论:①四边形CHFG是平行四边形,②AE=CG,③FE=FD,④四边形AFHE是菱形,其中正确的是( )
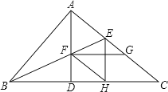
A.①②③④ B.②③④ C.①③④ D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
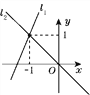
【题目】已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面网格中每个小正方形的边长为1. 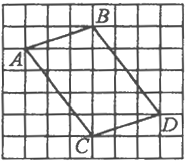
(1)线段CD是线段AB经过怎样的平移后得到的?
(2)线段AC是线段BD经过怎样的平移后得到的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在¨ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF,BF

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com