
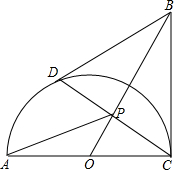
 已知:如图,CA=CB,且CA⊥CB,以AC为直径作半圆⊙O,点D为半圆⊙O上的一点,BD=BC,连接OB,交线段CD于点P.
已知:如图,CA=CB,且CA⊥CB,以AC为直径作半圆⊙O,点D为半圆⊙O上的一点,BD=BC,连接OB,交线段CD于点P.分析 (1)证明△OBC≌△OBD,则∠DBO=∠CBO,根据三线合一定理即可证明;
(2)作PE⊥AC于点E,利用面积公式求得PC,然后利用面积公式求得PE,再直角△OPE中利用勾股定理求得OE,则AE即可求得,利用三角函数定义求解.
解答 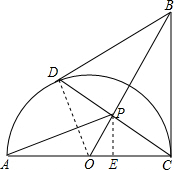 解:(1)连接OD.
解:(1)连接OD.
在△OBC和△OBD中,
$\left\{\begin{array}{l}{OB=OB}\\{OD=OC}\\{BD=BC}\end{array}\right.$,
∴△OBC≌△OBD,
∴∠DBO=∠CBO,
又∵BD=BC,即△BCD是等腰三角形,
∴DP=PC;
(2)作PE⊥AC于点E.
设半径是r,则OC=r,BC=2r,
在直角△OBC中,OB=$\sqrt{{r}^{2}+(2r)^{2}}$=$\sqrt{5}$r.
∵S△OBC=$\frac{1}{2}$OC•BC=$\frac{1}{2}$OB•PC,
∴PC=$\frac{OC•BC}{OB}$=$\frac{r•2r}{\sqrt{5}r}$=$\frac{2\sqrt{5}}{5}$r.
同理OP=$\sqrt{O{C}^{2}-P{C}^{2}}$=$\sqrt{{r}^{2}-(\frac{2\sqrt{5}}{5}r)^{2}}$=$\frac{\sqrt{5}}{5}$r.
PE=$\frac{OP•PC}{OC}$=$\frac{\frac{\sqrt{5}}{5}r•\frac{2\sqrt{5}}{5}r}{r}$=$\frac{2}{5}$r.
在直角△OPE中,OE=$\sqrt{O{P}^{2}-P{E}^{2}}$=$\sqrt{(\frac{\sqrt{5}}{5}r)^{2}-(\frac{2}{5}r)^{2}}$=$\frac{1}{5}$r.
则AE=r+$\frac{1}{5}$r=$\frac{6}{5}$r.
则tan∠OAP=$\frac{PE}{AE}$=$\frac{\frac{2}{5}r}{\frac{6}{5}r}$=$\frac{1}{3}$.
点评 本题考查了三角函数的定义以及等腰三角形的性质,正确理解三角函数的定义,正确作出辅助线是关键.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源:2016-2017学年吉林省七年级下学期期中数学模拟试卷(四)(解析版) 题型:单选题
甲、乙、丙三种商品,若购买甲3件、乙2件、丙1件,共需315元钱,购甲1件、乙2件、丙3件共需285元钱,那么购甲、乙、丙三种商品各一件共需多少钱( )
A. 128元 B. 130元 C. 150 元 D. 160元
查看答案和解析>>
科目:初中数学 来源:2017届山东省中考模拟数学试卷(解析版) 题型:单选题
将下列图形绕其对角线的交点逆时针旋转90°,所得图形一定与原图形重合的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
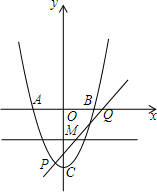 如图,抛物线y=x2-4分别交x轴于A、B,交y轴于C,P为第三象限的抛物线上一点,过P点的直线y=kx-3交直线y=-2于点M,交抛物线于另一点Q,若P、Q两点关于M成中心对称,求k的值.
如图,抛物线y=x2-4分别交x轴于A、B,交y轴于C,P为第三象限的抛物线上一点,过P点的直线y=kx-3交直线y=-2于点M,交抛物线于另一点Q,若P、Q两点关于M成中心对称,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
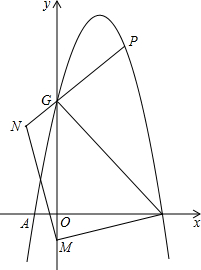 抛物线y=-x2+3x+4与x轴交于A,B两点,与y轴交于点C,如图,点M为y轴负半轴上一动点,点N在y轴左侧,MN⊥MB,MN=MB,连接NC交抛物线于点P,求点P的坐标.
抛物线y=-x2+3x+4与x轴交于A,B两点,与y轴交于点C,如图,点M为y轴负半轴上一动点,点N在y轴左侧,MN⊥MB,MN=MB,连接NC交抛物线于点P,求点P的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
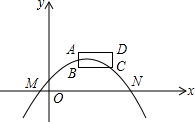 如图,矩形ABCD在平面直角坐标系的第一象限内,BC∥x轴,AB=1,BC=2,点B的坐标为(2,1),抛物线y=ax2+bx+c(a≠0)的顶点总是在矩形ABCD内部(包括边界),且与x轴的两个交点分别是点M(x1,0)、N(x2、0),其中-2≤x1≤-1,下列说法:①abc<0;②2a+b≤0;③当k<1时,方程ax2+bx+c-k=0总有两个不相等的实数根;④a的取值范围是-$\frac{2}{9}≤a≤-\frac{1}{36}$;其中正确的是①③④.
如图,矩形ABCD在平面直角坐标系的第一象限内,BC∥x轴,AB=1,BC=2,点B的坐标为(2,1),抛物线y=ax2+bx+c(a≠0)的顶点总是在矩形ABCD内部(包括边界),且与x轴的两个交点分别是点M(x1,0)、N(x2、0),其中-2≤x1≤-1,下列说法:①abc<0;②2a+b≤0;③当k<1时,方程ax2+bx+c-k=0总有两个不相等的实数根;④a的取值范围是-$\frac{2}{9}≤a≤-\frac{1}{36}$;其中正确的是①③④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
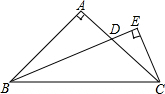 如图,△ABC中,AB=AC,∠BAC=90°,D是AC上一点,且CE⊥BD于点E,CE=$\frac{1}{2}$BD,求证:BD平分∠ABC.
如图,△ABC中,AB=AC,∠BAC=90°,D是AC上一点,且CE⊥BD于点E,CE=$\frac{1}{2}$BD,求证:BD平分∠ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com