
【题目】如图1,在平面直角坐标系中,![]() .
.
(1)求![]() 的面积;
的面积;
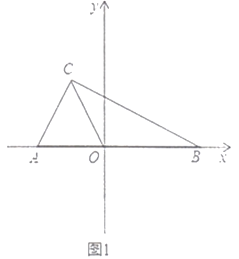
(2)点![]() 为坐标轴上一点,若
为坐标轴上一点,若![]() 的面积恰好是
的面积恰好是![]() 面积的一半,求点
面积的一半,求点![]() 的坐标.
的坐标.
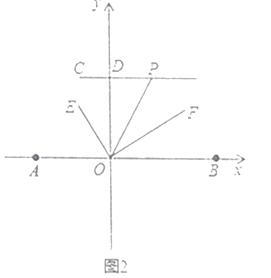
(3)如图2,过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 为
为![]() 延长线上的一动点,连接
延长线上的一动点,连接![]() 平分
平分![]() .当点
.当点![]() 运动时,
运动时,![]() 与
与![]() 度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.
度数之间的数量关系是否会改变?若不变,请直接写出其数量关系;若改变,请说明理由.
【答案】(1)5;(2)![]() 或
或![]() (0,5)或(0,-5);(3)
(0,5)或(0,-5);(3)![]() 与
与![]() 度数之间的数量关系不变,
度数之间的数量关系不变,![]() .
.
【解析】
(1)根据三角形的面积公式计算即可.
(2)分两种情形分别构建方程即可解决问题.
(3)根据平行线的性质及证明∠1=∠3即可解决问题.
![]() 如图1,过点
如图1,过点![]() 作
作![]() 轴,重足为
轴,重足为![]()
![]() ,
,
![]() ,
,
![]()
![]() ;
;

![]() 如图1,过点
如图1,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]()
![]()
![]()
由![]() 知
知![]() ,
,
![]()
①当点![]() 在
在![]() 轴上时,设
轴上时,设![]()
![]()
![]()
解得:![]()
![]() 的坐标为
的坐标为![]()
②当点![]() 在
在![]() 轴上时,设
轴上时,设![]()
![]()
![]()
解得:![]()
![]() 的坐标为
的坐标为![]()
点![]() 的坐标为
的坐标为![]() 或
或![]()
(3)结论:∠OPD=2∠DOE.
理由:如图2,
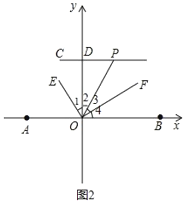
∵OE平分∠AOP,
∴∠AOE=∠POE=∠1+∠2,
∵OF⊥OE,
∴∠1+∠2+∠3=90°,∠4+∠AOE=90°,
∴∠3=∠4,
∵CD⊥y轴,
∴CD∥AB,
∴∠OPD=∠POB=2∠3,
∵∠1+∠2+∠3=90°,∠2+∠3+∠4=90°,
∴∠1+∠2+∠3=∠2+2∠3,
∴∠1=∠3,
由∠DOE=∠1,∠OPD=∠POB=2∠1
∴∠OPD=2∠DOE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为常分数,如: ![]() =
= ![]() =2+
=2+ ![]() =2
=2 ![]() .我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如
.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如 ![]() ,
,![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如:![]() ,
,![]() 这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如:
这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).如:![]()
![]() =1-
=1-![]() ;
;
解决下列问题:
(1)分式 ![]() 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);
(2)![]() 将假分式化为带分式;
将假分式化为带分式;
(3)如果 x 为整数,分式 ![]() 的值为整数,求所有符合条件的 x 的值.
的值为整数,求所有符合条件的 x 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年4月份的尼泊尔强震曾经导致珠峰雪崩,在珠峰抢险时,需8组登山队员步行运送物资,要求每组分配的人数相同,若按每组人数比预定人数多分配1人,则总数会超过100人;若按每组人数比预定人数少分配1人,则总数不够90人,那么预定每组分配的人数是( )
A. 10 B. 11 C. 12 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
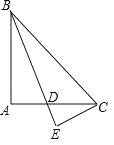
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=10,则CE=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,在
,在![]() 的外部作等边三角形
的外部作等边三角形![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
①补全图2;
②若![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式;
(2)农经公司应该如何确定这批农产品的销售价格,才能使日销售利润最大?
(3)若农经公司每销售1千克这种农产品需支出a元(a>0)的相关费用,当40≤x≤45时,农经公司的日获利的最大值为2430元,求a的值.(日获利=日销售利润﹣日支出费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病,呼吸道疾病等,给人们造成困扰.为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查表如图所示),并根据调查结果绘制了如下尚不完整的统计图.

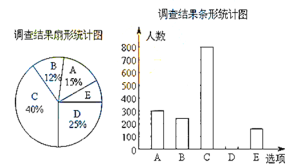
根据以上统计图,解答下列问题:
(1)本次接受调查的市民共有_________人;
(2)扇形统计图中,扇形![]() 的圆心角度数是__________;
的圆心角度数是__________;
(3)请补全条形统计图;
(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,过△ABC的顶点B作直线![]() ,且点A到
,且点A到![]() 的距离为2,点C到
的距离为2,点C到![]() 的距离为3,则AC的长是( )
的距离为3,则AC的长是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(﹣2,0),B(2,2),与y轴交于点C.
(1)求抛物线y=ax2+bx+2的函数表达式;
(2)若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;
(3)在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com