
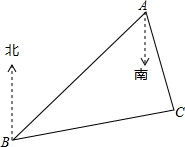
 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB的度数.
如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB的度数. 分析 根据方向角的定义,可得∠BAE=45°,∠CAE=15°,∠DBC=80°,然后根据平行线的性质与三角形内角和定理即可求解.
解答 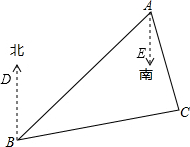 解:如图,根据方向角的定义,可得∠BAE=45°,∠CAE=15°,∠DBC=80°.
解:如图,根据方向角的定义,可得∠BAE=45°,∠CAE=15°,∠DBC=80°.
∵∠BAE=45°,∠EAC=15°,
∴∠BAC=∠BAE+∠EAC=45°+15°=60°.
∵AE,DB是正南正北方向,
∴BD∥AE,
∵∠DBA=∠BAE=45°,
又∵∠DBC=80°,
∴∠ABC=80°-45°=35°,
∴∠ACB=180°-∠ABC-∠BAC=180°-60°-35°=85°.
点评 本题主要考查了方向角的定义,平行线的性质以及三角形的内角和定理,正确理解定义是解题的关键.


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | ±4 | C. | 32 | D. | 64 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,按以下步骤作图:①分别以A、B为圆心,大于$\frac{1}{2}AB$的长为半径画弧,相交于两点M、N;②联结MN,直线MN交△ABC的边AC与点D,联结BD.如果此时测得∠A=34°,BC=CD.求∠ABC与∠C的度数.
如图,在△ABC中,按以下步骤作图:①分别以A、B为圆心,大于$\frac{1}{2}AB$的长为半径画弧,相交于两点M、N;②联结MN,直线MN交△ABC的边AC与点D,联结BD.如果此时测得∠A=34°,BC=CD.求∠ABC与∠C的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
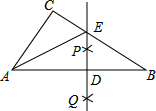 如图,在△ABC中,∠C=90°,∠CAB=62°,按以下步骤作图:
如图,在△ABC中,∠C=90°,∠CAB=62°,按以下步骤作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com