
分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=($\frac{x+2}{x-2}$-$\frac{1}{x-2}$)•$\frac{(x+2)(x-2)}{x}$
=$\frac{x+1}{x-2}$•$\frac{(x+2)(x-2)}{x}$
=$\frac{(x+1)(x+2)}{x}$,
当x=-$\frac{1}{2}$时,原式=$\frac{(-\frac{1}{2}+1)(-\frac{1}{2}+2)}{-\frac{1}{2}}$=-$\frac{3}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,AB是半圆O的直径,点P从点A出发,沿A→B→O→A的路径运动一周.设OP为s,运动时间为t,则下列图形能大致地刻画s与t之间关系的是( )
如图所示,AB是半圆O的直径,点P从点A出发,沿A→B→O→A的路径运动一周.设OP为s,运动时间为t,则下列图形能大致地刻画s与t之间关系的是( )| A. |  | B. | 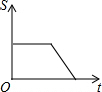 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-x+m与y轴交于点B,与正比例函数y=$\frac{1}{2}$x的图象交于点P(2,n).
如图,一次函数y=-x+m与y轴交于点B,与正比例函数y=$\frac{1}{2}$x的图象交于点P(2,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
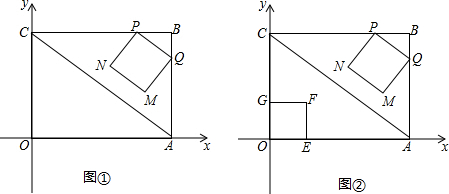
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com