
 如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C的度数为( )
如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C的度数为( )| A. | 135° | B. | 120° | C. | 90° | D. | 105° |
分析 连接EE′,如图,根据旋转的性质得BE=BE′=2,AE=CE′=1,∠EBE′=90°,则可判断△BEE′为等腰直角三角形,根据等腰直角三角形的性质得EE′=$\sqrt{2}$BE=2$\sqrt{2}$,∠BE′E=45°,在△CEE′中,由于CE′2+EE′2=CE2,根据勾股定理的逆定理得到△CEE′为直角三角形,即∠EE′C=90°,然后利用∠BE′C=∠BE′E+∠CE′E求解.
解答 解:连接EE′,如图,
∵△ABE绕点B顺时针旋转90°得到△CBE′,
∴BE=BE′=2,AE=CE′=1,∠EBE′=90°,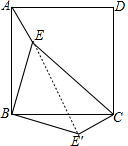
∴△BEE′为等腰直角三角形,
∴EE′=$\sqrt{2}$BE=2$\sqrt{2}$,∠BE′E=45°,
在△CEE′中,CE=3,CE′=1,EE′=2$\sqrt{2}$,
∵12+(2$\sqrt{2}$)2=32,
∴CE′2+EE′2=CE2,
∴△CEE′为直角三角形,
∴∠EE′C=90°,
∴∠BE′C=∠BE′E+∠CE′E=135°.
故选:A.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了勾股定理的逆定理、等腰直角三角形的判定与性质和正方形的性质.


科目:初中数学 来源: 题型:解答题
 如图,AD为△ABC的中线,BE为△ABD的中线
如图,AD为△ABC的中线,BE为△ABD的中线查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+b)2=a2+b2 | B. | (x-3y)2=x2-3xy+9y2 | ||
| C. | (6a3-4a2+2a)÷2a=3a2-2a | D. | ab2÷a=b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 节约汽油10公斤和浪费酒精10公斤 | B. | 向东走5公里和向南走5公里 | ||
| C. | 收入300元和支出500元 | D. | 身高180cm和身高90cm |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月月考数学试卷(解析版) 题型:判断题
定义:我们把三角形被一边中线分成的两个三角形叫做“友好三角形”.
性质:如果两个三角形是“友好三角形”,那么这两个三角形的面积相等.
理【解析】
如图①,在△ABC中,CD是AB边上的中线,那么△ACD和△BCD是“友好三角形”,并且S△ACD=S△BCD.
应用:如图②,在矩形ABCD中,AB=4,BC=6,点E在AD上,点F在BC上,AE=BF,AF与BE交于点O.
(1)求证:△AOB和△AOE是“友好三角形”;
(2)连接OD,若△AOE和△DOE是“友好三角形”,求四边形CDOF的面积.

查看答案和解析>>
科目:初中数学 来源:2017届江苏省九年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,⊙O的直径CD=5cm,弦AB⊥CD,垂足为M,OM︰OD=3︰5.则AB的长是( )

A. 2 cm B. 3cm C. 4cm D. 2
cm B. 3cm C. 4cm D. 2 cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com