
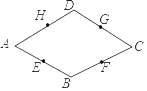
【题目】已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,为测量某建筑物AB的高度,在离该建筑物底部20m的点C处,目测建筑物顶端A处,视线与水平线夹角∠ADE为38.5°,目高CD为1.6m.求建筑物AB的高度.(结果精确到1m)(参考数据:sin38.5°=0.623,cos38.5°=0.783,tan38.5°=0.795)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形 ABCD 中,AE 平分∠BAD 交边 BC 于 E,DF 平分∠ADC 交边 BC 于 F,若 AD=11,EF=5,则 AB= ___.
查看答案和解析>>
科目:初中数学 来源: 题型:
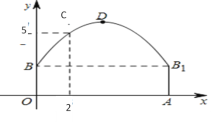
【题目】如图隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为2m,到地面OA的距离为5m.
x2+bx+c表示,且抛物线上的点C到OB的水平距离为2m,到地面OA的距离为5m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)该隧道内设双行道,一辆货车高4m,宽2.5m,能否安全通过,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=x2﹣4x+3
(1)求其图象与x轴交点A、B的坐标(A在B左边);
(2)在坐标系中画出函数图象;
(3)若函数图形的顶点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,给出如下定义:
对于⊙C及⊙C外一点P,M,N是⊙C上两点,当∠MPN最大,称∠MPN为点P关于⊙C的“视角”.直线l与⊙C相离,点Q在直线l上运动,当点Q关于⊙C的“视角”最大时,则称这个最大的“视角”为直线l关于⊙C的“视角”.
(1)如图,⊙O的半径为1,
①已知点A(1,1),直接写出点A关于⊙O的“视角”;已知直线y = 2,直接写出直线y = 2关于⊙O的“视角”;
②若点B关于⊙O的“视角”为60°,直接写出一个符合条件的B点坐标;
(2)⊙C的半径为1,
①C的坐标为(1,2),直线l: y=kx + b(k > 0)经过点D(![]() ,0),若直线l关于⊙C的“视角”为60°,求k的值;
,0),若直线l关于⊙C的“视角”为60°,求k的值;
②圆心C在x轴正半轴上运动,若直线y =![]() x +
x +![]() 关于⊙C的“视角”大于120°,直接写出圆心C的横坐标xC的取值范围.
关于⊙C的“视角”大于120°,直接写出圆心C的横坐标xC的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在改革开放30年纪念活动中,某校学生会就同学们对我国改革开放30年所取得的辉煌成就的了解程度进行了随机抽样调查,并将调查结果绘制成如图所示的统计图的一部分.
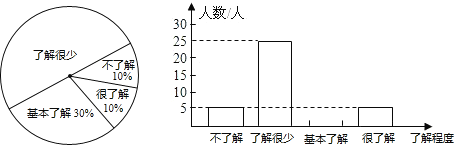
根据统计图中的信息,解答下列问题:
(1)本次抽样调查的样本容量是 .调查中“了解很少”的学生占 %;
(2)补全条形统计图;
(3)若全校共有学生1300人,那么该校约有多少名学生“很了解”我国改革开放30年来取得的辉煌成就.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中任取一个数作为k的值,则能使分式方程![]() 有非负实数解且使二次函数y=x2+2x﹣k﹣1的图象与x轴无交点的概率为( )
有非负实数解且使二次函数y=x2+2x﹣k﹣1的图象与x轴无交点的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.0
D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com