
 PC•CQ=-6t2+24t
PC•CQ=-6t2+24t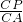 =
=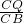 ,即
,即 ,
,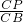 =
=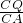 ,即
,即 ,
,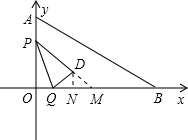 若PD∥AB,则∠QMD=∠B,又∵∠QDM=∠C=90°,
若PD∥AB,则∠QMD=∠B,又∵∠QDM=∠C=90°,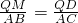 ,
,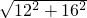 =20,
=20,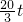 ,
,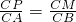 ,即
,即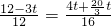 ,
,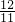 ,
, ,CQ=4t=
,CQ=4t=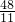 ,
, ,即
,即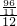 =
= ,
, ,
,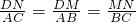 ,即
,即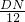 =
=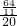 =
=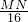 ,
,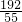 ,MN=
,MN=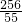 ,
, t=
t=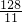 ,
,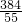 .
.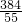 ,
,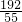 ).
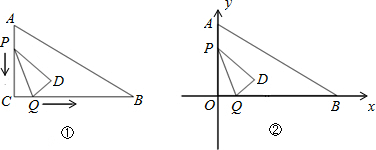
). t,再由CQ+QM表示出CM,由PD与AB平行,根据两直线平行得到两对同位角相等,从而得出三角形PCM与三角形ABC相似,由相似得比例,把CM,CP,CA及CB的长代入列出关于t的方程,求出方程的解得到t的值,从而确定出CP,PD及CQ的长,进而确定出PM的长,得出DM的长,过D作x轴的垂直交x轴于N,由DM与AB平行得出两对同位角相等,可得三角形DMN与三角形ABC相似,根据相似得比例,可求出MN及DN的长,进而得出CN的长,得出点D的坐标.
t,再由CQ+QM表示出CM,由PD与AB平行,根据两直线平行得到两对同位角相等,从而得出三角形PCM与三角形ABC相似,由相似得比例,把CM,CP,CA及CB的长代入列出关于t的方程,求出方程的解得到t的值,从而确定出CP,PD及CQ的长,进而确定出PM的长,得出DM的长,过D作x轴的垂直交x轴于N,由DM与AB平行得出两对同位角相等,可得三角形DMN与三角形ABC相似,根据相似得比例,可求出MN及DN的长,进而得出CN的长,得出点D的坐标.

科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| OC2 |
| 1 |
| OD2 |
| 1 |
| OM2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com