
【题目】已知圆O的直径AB=12,点C是圆上一点,且∠ABC=30°,点P是弦BC上一动点,过点P作PD⊥OP交圆O于点D.

(1)如图1,当PD∥AB 时,求PD的长;
(2)如图2,当BP平分∠OPD时,求PC的长.
【答案】(1)PD=![]() ;(2)PC=3
;(2)PC=3![]()
【解析】
(1)先判断出∠POB=90°,进而求出OP=OBtan30°=2![]() 最后用勾股定理即可得出结论;
最后用勾股定理即可得出结论;
(2)先求出OH=![]() OB=3,BH=OBcos30°=3
OB=3,BH=OBcos30°=3![]() ,进而求出CH=BH=3
,进而求出CH=BH=3![]() ,即可得出结论.
,即可得出结论.
解:如图1,连接OD .
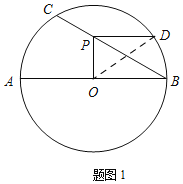
∵直径AB=12
∴OB=OD=6
∵PD⊥OP
∴∠DPO=90°
∵PD∥AB
∴∠DPO+∠POB=180°
∴∠POB=90°
又∵∠ABC=30°,OB=6
∴![]() ,
,
∵在Rt△POD 中,PO2+PD2=OD2
∴![]() ,
,
∴![]() ;
;
(2)如图2,过点O 作OH⊥BC,垂足为H
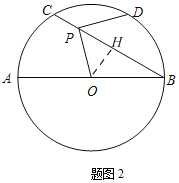
∵OH⊥BC
∴∠OHB=∠OHP=90°
∵∠ABC=30°,OB=6
∴![]() ,
,![]() ,
,
∵在⊙O 中,OH⊥BC
∴![]() .
.
∵BP 平分∠OPD
∴∠BPO=![]() ∠DPO=45°,
∠DPO=45°,
∴PH=OHcot45°=3
∴PC=CH-PH=![]() .
.


科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查![]() 每个被调查的学生必须选择而且只能选择其中一门
每个被调查的学生必须选择而且只能选择其中一门![]() 对调查结果进行整理,绘制成如下两幅不完整的统计图
对调查结果进行整理,绘制成如下两幅不完整的统计图![]() 请结合图中所给信息解答下列问题:
请结合图中所给信息解答下列问题:


![]() 本次调查的学生共有______人,在扇形统计图中,m的值是______.
本次调查的学生共有______人,在扇形统计图中,m的值是______.
![]() 分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
![]() 该校共有学生2000人,估计该校约有多少人选修乐器课程?
该校共有学生2000人,估计该校约有多少人选修乐器课程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).
(1)求证:方程有两个不相等的实数根;
(2)设x1,x2为方程的两个实数根,且x1+2x2=14,试求出方程的两个实数根和k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题的大意是:有一块三角形沙田,三条边长分别为5里;12里;13里,问这块沙田面积有多大?题中的1里=0.5千米,则该沙田的面积为( )
A.3平方千米B.7.5平方千米C.15平方千米D.30平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,线段
,线段![]() ,
,![]() ,一机器人
,一机器人![]() 在点
在点![]() 处.
处.
(1)若![]() ,求线段
,求线段![]() 的长.
的长.
(2)在(1)的条件下,若机器人![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿着
的速度沿着![]() 的三条边逆时针走一圈后回到点
的三条边逆时针走一圈后回到点![]() ,设行走的时间为
,设行走的时间为![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 是以
是以![]() 点为直角顶点的直角三角形?
点为直角顶点的直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题:在首届“一带一路”国际合作高峰论坛举办之后,某公司准备生产甲、乙两种商品销往“一带一路”沿线国家和地区,原计划生产甲商品和乙商品共210吨,采用新技术后,实际产量为230吨,其中甲商品超产5%,乙商品超产15%,求该公司实际生产甲、乙两种商品各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:![]() ≈1.4)( )
≈1.4)( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的治理西流湖水质,保护环境,市治污公司决定购买 10 台污水处理设备.现有 A、B 两种型号的设备,其中每台的价格,月处理污水量如下表:
A 型 | B 型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 200 |
经调查:购买一台 A 型设备比购买一台 B 型设备多 2 万元,购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元.
(1)求 a,b 的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过 105 万元,你认为该公司 有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于 2040 吨,为了节 约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com