
 我们知道,代数恒等式都可以用面积的方法来加以验证它的正确性,用图形的拼接我们可以发现更多的代数恒等式,图是由4个长为m、宽为n的小长方形拼成的大长方形.
我们知道,代数恒等式都可以用面积的方法来加以验证它的正确性,用图形的拼接我们可以发现更多的代数恒等式,图是由4个长为m、宽为n的小长方形拼成的大长方形.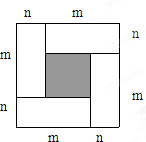 ;
;

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建省晋江市八年级上学期期末跟踪测试数学试卷(带解析) 题型:解答题
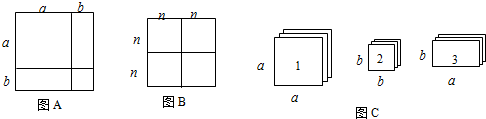
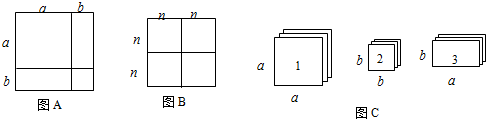
我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A
可以用来解释 ,实际上利用一些卡片拼成的图形面积也可以
,实际上利用一些卡片拼成的图形面积也可以
对某些二次三项式进行因式分解.
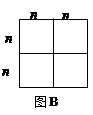

(1)图B可以解释的代数恒等式是_____________ ;
(2)现有足够多的正方形和矩形卡片,如图C:
①.若要拼出一个面积为 的矩形,则需要1号卡片 张,2号卡片 张,
的矩形,则需要1号卡片 张,2号卡片 张,
3号卡片 张;
②.试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为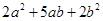 ,并利用你画的图形面积对
,并利用你画的图形面积对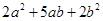 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源:2014届福建省晋江市八年级上学期期末跟踪测试数学试卷(解析版) 题型:解答题
我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A
可以用来解释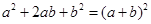 ,实际上利用一些卡片拼成的图形面积也可以
,实际上利用一些卡片拼成的图形面积也可以
对某些二次三项式进行因式分解.
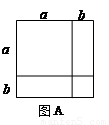
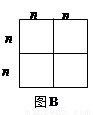

(1)图B可以解释的代数恒等式是_____________ ;
(2)现有足够多的正方形和矩形卡片,如图C:
①.若要拼出一个面积为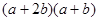 的矩形,则需要1号卡片 张,2号卡片 张,
的矩形,则需要1号卡片 张,2号卡片 张,
3号卡片 张;
②.试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为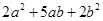 ,并利用你画的图形面积对
,并利用你画的图形面积对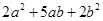 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com