
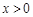 ),四边形BCDP的面积为y cm2.
),四边形BCDP的面积为y cm2.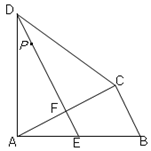
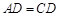 ,
,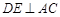 ,∴DE垂直平分AC,
,∴DE垂直平分AC,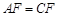 ,∠DFA=∠DFC =90°,∠DAF=∠DCF.
,∠DFA=∠DFC =90°,∠DAF=∠DCF.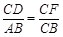 ,即
,即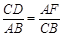 .
.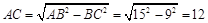 ,∴
,∴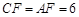 .
.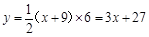 (
(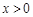 ).
). 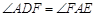 ,
,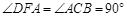 ,得△DAF∽△ABC.
,得△DAF∽△ABC.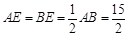 ,EF=
,EF=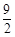 .
.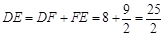 .
.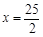 时,△PBC的周长最小,此时
时,△PBC的周长最小,此时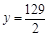 .
.

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
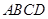 的边长为4,
的边长为4,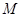 、
、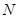 分别是
分别是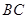 、
、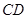 上的两个动点,当
上的两个动点,当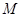 点在
点在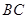 上运动时,始终保持
上运动时,始终保持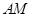 和
和 垂直,
垂直,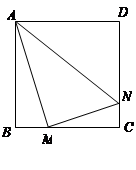
 ;
;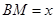 ,梯形
,梯形 的面积为
的面积为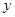 ,求
,求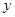 与
与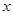 之间的函数关系式;当
之间的函数关系式;当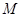 点运动到什么位置时,四边形
点运动到什么位置时,四边形 面积最大,并求出最大面积;
面积最大,并求出最大面积;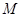 点运动到什么位置时,
点运动到什么位置时, ?并求出此时BM的长.
?并求出此时BM的长.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
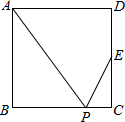
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
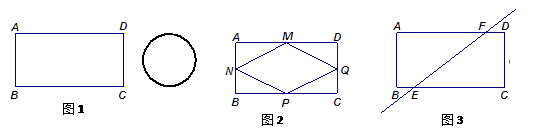
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
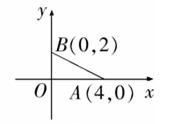
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com