
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬AB=BC£¬”ĻABC=90”ć£®ŅŌABĪŖŠ±±ß×÷µČŃüÖ±½ĒČż½ĒŠĪADB£®µćPŹĒÖ±ĻßDBÉĻŅ»øö¶Æµć£¬Į¬½ÓAP£¬×÷PE”ĶAP½»BCĖłŌŚµÄÖ±ĻßÓŚµćE£®
£Ø1£©ČēĶ¼1£¬µćPŌŚBDµÄŃÓ³¤ĻßÉĻ£¬PE”ĶEC£¬AD=1£¬Ö±½ÓŠ“³öPEµÄ³¤£»
£Ø2£©µćPŌŚĻ߶ĪBDÉĻ£Ø²»ÓėB£¬DÖŲŗĻ£©£¬ŅĄĢāŅā£¬½«Ķ¼2²¹Č«£¬ĒóÖ¤£ŗPA=PE£»
£Ø3£©µćPŌŚDBµÄŃÓ³¤ĻßÉĻ£¬ŅĄĢāŅā£¬½«Ķ¼3²¹Č«£¬²¢ÅŠ¶ĻPA=PEŹĒ·ńČŌČ»³ÉĮ¢£®
”¾“š°ø”æ
£Ø1£©
½ā£ŗ”ßAD=DB=1£¬”ĻADB=90”ć£¬
”ą”ĻABP=45”ć£¬AB= ![]() =
= ![]() £¬
£¬
”ßPE”ĶAP£¬AB”ĶBC£¬
”ąPA”ĪEC£¬
”ąPA”ĶAB£¬
”ąĖıߊĪABEPŹĒ¾ŲŠĪ£¬
”ß”ĻABP=45”ć£¬
”ąPA=AB£¬
”ąĖıߊĪABEPŹĒÕż·½ŠĪ£¬
”ąPE=AB= ![]()
£Ø2£©
½ā£ŗ”ß”÷ABCŗĶ”÷ADBŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻADB=90”ć£¬”ĻDAB=”ĻDBA=45”ć£¬
”ą”ĻPBN=45”ć
”ąPE”ĶAP£¬”ĻDAP=”ĻBPE=90”ć©”ĻDPA£¬
”ß”ĻPAM=45”ć©”ĻDAP£¬”ĻPEN=45”ć©”ĻBPE£¬
”ą”ĻPAM=”ĻPEN£¬
¹żP×÷PM”ĶABÓŚµćM£¬¹żP×÷PN”ĶBCÓŚµćN£¬

ŌņPM=PN£¬”ĻBPN=45”ć£¬
ŌŚ”÷APMŗĶ”÷EPNÖŠ£¬  £¬
£¬
”ą”÷APM”Õ”÷EPN£¬
”ąPA=PE£»
£Ø3£©
½ā£ŗ”ß”÷ABCŗĶ”÷ADBŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻABD=45”ć£¬
”ą”ĻPBN=45”ć£¬”ĻABC=90”ć£¬
¹żP×÷PM”ĶABÓŚµćM£¬¹żP×÷PN”ĶBCÓŚµćN£¬
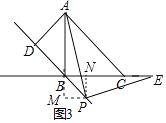
ŌņĖıߊĪBMPNŹĒ¾ŲŠĪ£¬
”ß”ĻNBP=45”ć£¬
”ąĖıߊĪBMPNŹĒÕż·½ŠĪ£¬
”ąPM=PN£¬
”ßAB”ĶBC£¬
”ą”ĻBAN=”ĻAPN£¬
”ßAP”ĶPE£¬
”ą”ĻAPN=”ĻE£¬
”ą”ĻBAP=”ĻE£¬
ŌŚ”÷AMPÓė”÷ENPÖŠ£¬  £¬
£¬
”ą”÷AMP”Õ”÷ENP£¬
”ąAP=PE£®
”¾½āĪö”æ£Ø1£©øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻABP=45”ć£¬øł¾Ż¹“¹É¶ØĄķµĆµ½AB= ![]() =
= ![]() £¬ĶĘ³öĖıߊĪABEPŹĒ¾ŲŠĪ£¬µĆµ½ĖıߊĪABEPŹĒÕż·½ŠĪ£¬ÓŚŹĒµĆµ½½įĀŪ£»£Ø2£©øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻADB=90”ć£¬”ĻDAB=”ĻDBA=45”ć£¬ĒóµĆ”ĻPBN=45”ć¹żP×÷PM”ĶABÓŚµćM£¬¹żP×÷PN”ĶBCÓŚµćN£¬ÓŚŹĒµĆµ½PM=PN£¬”ĻBPN=45”ćøł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹ¼“æɵƵ½½įĀŪ£»£Ø3£©øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻABD=45”ć£¬µĆµ½”ĻPBN=45”ć£¬”ĻABC=90”ć£¬¹żP×÷PM”ĶABÓŚµćM£¬¹żP×÷PN”ĶBCÓŚµćN£¬µĆµ½ĖıߊĪBMPNŹĒ¾ŲŠĪ£¬ĶĘ³öĖıߊĪBMPNŹĒÕż·½ŠĪ£¬µĆµ½PM=PN£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹ¼“æɵƵ½½įĀŪ£®
£¬ĶĘ³öĖıߊĪABEPŹĒ¾ŲŠĪ£¬µĆµ½ĖıߊĪABEPŹĒÕż·½ŠĪ£¬ÓŚŹĒµĆµ½½įĀŪ£»£Ø2£©øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻADB=90”ć£¬”ĻDAB=”ĻDBA=45”ć£¬ĒóµĆ”ĻPBN=45”ć¹żP×÷PM”ĶABÓŚµćM£¬¹żP×÷PN”ĶBCÓŚµćN£¬ÓŚŹĒµĆµ½PM=PN£¬”ĻBPN=45”ćøł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹ¼“æɵƵ½½įĀŪ£»£Ø3£©øł¾ŻµČŃüÖ±½ĒČż½ĒŠĪµÄŠŌÖŹµĆµ½”ĻABD=45”ć£¬µĆµ½”ĻPBN=45”ć£¬”ĻABC=90”ć£¬¹żP×÷PM”ĶABÓŚµćM£¬¹żP×÷PN”ĶBCÓŚµćN£¬µĆµ½ĖıߊĪBMPNŹĒ¾ŲŠĪ£¬ĶĘ³öĖıߊĪBMPNŹĒÕż·½ŠĪ£¬µĆµ½PM=PN£¬øł¾ŻČ«µČČż½ĒŠĪµÄŠŌÖŹ¼“æɵƵ½½įĀŪ£®
”¾æ¼µć¾«Īö”æÕĘĪÕµČŃüÖ±½ĒČż½ĒŠĪŗĶÕż·½ŠĪµÄÅŠ¶Ø·½·ØŹĒ½ā“š±¾ĢāµÄøł±¾£¬ŠčŅŖÖŖµĄµČŃüÖ±½ĒČż½ĒŠĪŹĒĮ½ĢõÖ±½Ē±ßĻąµČµÄÖ±½ĒČż½ĒŠĪ£»µČŃüÖ±½ĒČż½ĒŠĪµÄĮ½øöµ×½ĒĻąµČĒŅµČÓŚ45”ć£»ĻČÅŠ¶ØŅ»øöĖıߊĪŹĒ¾ŲŠĪ£¬ŌŁÅŠ¶Ø³öÓŠŅ»×éĮŚ±ßĻąµČ£»ĻČÅŠ¶ØŅ»øöĖıߊĪŹĒĮāŠĪ£¬ŌŁÅŠ¶Ø³öÓŠŅ»øö½ĒŹĒÖ±½Ē£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģx2©2x+m©1=0ÓŠĮ½øöŹµŹżøłx1 £¬ x2 £®
£Ø1£©ĒómµÄȔֵ·¶Ī§£»
£Ø2£©µ±x12+x22=6x1x2Ź±£¬ĒómµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻACB£½90”ć£¬AC£½BC£¬DĪŖ”÷ABCÄŚŅ»µć£¬”ĻCAD£½”ĻCBD£½15”ć£¬EĪŖADŃÓ³¤ĻßÉĻµÄŅ»µć£¬ĒŅCE£½AC.

(1)Ēó”ĻCDEµÄ¶ČŹż£»
(2)ČōµćMŌŚDEÉĻ£¬ĒŅDC£½DM£¬ĒóÖ¤£ŗME£½BD.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±Ļßy=2x+1ÓėĖ«ĒśĻßy= ![]() µÄŅ»øö½»µćĪŖA£Øm£¬©3£©£®
µÄŅ»øö½»µćĪŖA£Øm£¬©3£©£®
£Ø1£©ĒóĖ«ĒśĻߵıķ“ļŹ½£»
£Ø2£©¹ż¶ÆµćP£Øn£¬0£©£Øn£¼0£©ĒŅ“¹Ö±ÓŚxÖįµÄÖ±ĻßÓėÖ±Ļßy=2x+1ŗĶĖ«ĒśĻßy= ![]() µÄ½»µć·Ö±šĪŖB£¬C£¬µ±µćBĪ»ÓŚµćCÉĻ·½Ź±£¬Ö±½ÓŠ“³önµÄȔֵ·¶Ī§£®
µÄ½»µć·Ö±šĪŖB£¬C£¬µ±µćBĪ»ÓŚµćCÉĻ·½Ź±£¬Ö±½ÓŠ“³önµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠÕāŃłŅ»øöĪŹĢā£ŗĢ½¾æŗÆŹży= ![]() ©
© ![]() xµÄĶ¼ĻóÓėŠŌÖŹ£® Š”¶«øł¾ŻŃ§Ļ°ŗÆŹżµÄ¾Ń飬¶ŌŗÆŹży=
xµÄĶ¼ĻóÓėŠŌÖŹ£® Š”¶«øł¾ŻŃ§Ļ°ŗÆŹżµÄ¾Ń飬¶ŌŗÆŹży= ![]() ©
© ![]() xµÄĶ¼ĻóÓėŠŌÖŹ½ųŠŠĮĖĢ½¾æ£®
xµÄĶ¼ĻóÓėŠŌÖŹ½ųŠŠĮĖĢ½¾æ£®
ĻĀĆęŹĒŠ”¶«µÄĢ½¾æ¹ż³Ģ£¬Ēė²¹³äĶźÕū£¬²¢½ā¾öĻą¹ŲĪŹĢā£ŗ
£Ø1£©ŗÆŹży= ![]() ©
© ![]() xµÄ×Ō±äĮæxµÄȔֵ·¶Ī§ŹĒ£»
xµÄ×Ō±äĮæxµÄȔֵ·¶Ī§ŹĒ£»
£Ø2£©ĻĀ±ķŹĒyÓėxµÄ¼ø×é¶ŌÓ¦Öµ£¬ĒómµÄÖµ£»
x | ” | ©4 | ©3 | ©2 | © | ©1 | © | | 1 | 2 | 3 | 4 | ” |
y | ” | | | | | | | | | © | © | m | ” |
£Ø3£©ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ćč³öĮĖŅŌÉĻ±ķÖŠø÷¶Ō¶ŌÓ¦ÖµĪŖ×ų±źµÄµć£®øł¾ŻĆč³öµÄµć£¬»³öøĆŗÆŹżµÄĶ¼Ļó£» 
£Ø4£©½ųŅ»²½Ģ½¾æ·¢ĻÖ£¬øĆŗÆŹżĶ¼ĻóŌŚµŚ¶žĻóĻŽÄŚµÄ×īµĶµćµÄ×ų±źŹĒ£Ø©2£¬ ![]() £©£¬½įŗĻŗÆŹżµÄĶ¼Ļ󣬊“³öøĆŗÆŹżµÄĘäĖüŠŌÖŹ£ØŅ»Ģõ¼“æÉ£© £®
£©£¬½įŗĻŗÆŹżµÄĶ¼Ļ󣬊“³öøĆŗÆŹżµÄĘäĖüŠŌÖŹ£ØŅ»Ģõ¼“æÉ£© £®
£Ø5£©øł¾ŻŗÆŹżĶ¼Ļó¹ĄĖć·½³Ģ ![]() ©
© ![]() x=2µÄøłĪŖ £® £Ø¾«Č·µ½0.1£©
x=2µÄøłĪŖ £® £Ø¾«Č·µ½0.1£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
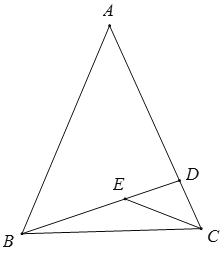
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬BD”ĶACÓŚD£®Čō”ĻA£ŗ”ĻABC£ŗ”ĻACB=3£ŗ4£ŗ5£¬EĪŖĻ߶ĪBDÉĻČĪŅ»µć£®
£Ø1£©ŹŌĒó”ĻABDµÄ¶ČŹż£»
£Ø2£©ĒóÖ¤£ŗ”ĻBEC£¾”ĻA£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ĆūĶ¬Ń§Ļą¾ą20m£¬ĖūĆĒĶ¬Ź±³ö·¢£¬Ķ¬Ļņ¶ųŠŠ£¬¼×ŌŚŅŅŗó£¬Ķ¼ÖŠL1”¢L2·Ö±š±ķŹ¾ĖūĆĒ¶žČĖµÄĀ·³ĢÓėŹ±¼äµÄ¹ŲĻµ£¬æ“Ķ¼»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©20sŹ±¼×ÅÜĮĖ¶ąÉŁĆ×£æŅŅÅÜĮĖ¶ąÉŁĆ×£æ
£Ø2£©¼×ÓĆ¼øĆėÖÓæÉ×·ÉĻŅŅ£æ

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĄ×“ļ¶žĪ¬Ę½Ćę¶ØĪ»µÄÖ÷ŅŖŌĄķŹĒ£ŗ²āĮæÄæ±źµÄĮ½øöŠÅĻ¢ØD¾ąĄėŗĶ½Ē¶Č£¬Äæ±źµÄ±ķŹ¾·½·ØĪŖ![]() £¬ĘäÖŠ£¬m±ķŹ¾Äæ±źÓėĢ½²āĘ÷µÄ¾ąĄė£»
£¬ĘäÖŠ£¬m±ķŹ¾Äæ±źÓėĢ½²āĘ÷µÄ¾ąĄė£»![]() ±ķŹ¾ŅŌÕż¶«ĪŖŹ¼±ß£¬ÄꏱÕėŠż×ŖŗóµÄ½Ē¶Č£®ČēĶ¼£¬Ą×“ļĢ½²āĘ÷ĻŌŹ¾ŌŚµćA£¬B£¬C“¦ÓŠÄæ±ź³öĻÖ£¬ĘäÖŠ£¬Äæ±źAµÄĪ»ÖƱķŹ¾ĪŖ
±ķŹ¾ŅŌÕż¶«ĪŖŹ¼±ß£¬ÄꏱÕėŠż×ŖŗóµÄ½Ē¶Č£®ČēĶ¼£¬Ą×“ļĢ½²āĘ÷ĻŌŹ¾ŌŚµćA£¬B£¬C“¦ÓŠÄæ±ź³öĻÖ£¬ĘäÖŠ£¬Äæ±źAµÄĪ»ÖƱķŹ¾ĪŖ![]() £¬Äæ±źCµÄĪ»ÖƱķŹ¾ĪŖ
£¬Äæ±źCµÄĪ»ÖƱķŹ¾ĪŖ![]() £®ÓĆÕāÖÖ·½·Ø±ķŹ¾Äæ±źBµÄĪ»ÖĆ£¬ÕżČ·µÄŹĒ£Ø £©
£®ÓĆÕāÖÖ·½·Ø±ķŹ¾Äæ±źBµÄĪ»ÖĆ£¬ÕżČ·µÄŹĒ£Ø £©

A. (-4, 150”ć) B. (4, 150”ć) C. (-2, 150”ć) D. (2, 150”ć)
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬±ß³¤·Ö±šĪŖ2ŗĶ4µÄĮ½øöČ«µČČż½ĒŠĪ£¬æŖŹ¼ĖüĆĒŌŚ×ó±ßÖŲµž£¬“ó”÷ABC¹Ģ¶Ø²»¶Æ£¬Č»ŗó°ŃŠ””÷A”äB”äC”ä×Ō×óĻņÓŅĘ½ŅĘ£¬Ö±ÖĮŅʵ½µćB”äµ½CÖŲŗĻŹ±Ķ£Ö¹£¬É芔ȿ½ĒŠĪŅĘ¶ÆµÄ¾ąĄėĪŖx£¬Į½øöČż½ĒŠĪµÄÖŲŗĻ²æ·ÖµÄĆ껿ĪŖy£¬Ōņy¹ŲÓŚxµÄŗÆŹżĶ¼ĻóŹĒ£Ø £©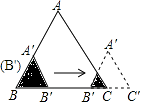
A.
B.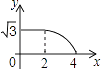
C.
D.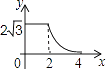
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com