
【题目】在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2 个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢,赢的一方得电影票.
(1)游戏规则1:两人各摸1个球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
(2)游戏规则2; 两人同时各摸1个球,若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏小明赢得电影票的概率为 .
【答案】(1)此游戏不公平(2)![]()
【解析】试题分析:(1)游戏是否公平,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
(2)本题可通过列表法或画树状图法来求,解题时要注意:(1)摸出小球后记下颜色放回与不放回的区别;(2)把红球标记为红1和红2,保证每次摸球的可能性相等.
试题解析:
(1)此游戏不公平.
理由如下:列树状图如下,
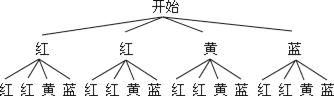
列表如下,
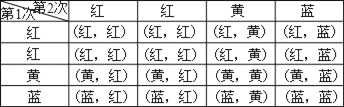
由上述树状图或表格知:所有可能出现的结果共有16种.
P(小明赢)=![]() ,P(小亮赢)=
,P(小亮赢)=![]() .
.
∴此游戏对双方不公平,小亮赢的可能性大;
(2)列表如下:
红1 | 红2 | 黄 | 蓝 | |
红1 | 红1红1 | 红1红2 | 红1黄 | 红1蓝 |
红2 | 红2红1 | 红2红2 | 红2黄 | 红2蓝 |
黄 | 黄 红1 | 黄 红2 | 黄黄 | 黄蓝 |
蓝 | 蓝 红1 | 蓝 红2 | 蓝黄 | 蓝蓝 |
由表格可知,共有16种等可能的结果,其中两球颜色相同的情况有6种,故小明赢得门票的概率为![]() .
.
故答案为: ![]() .
.


科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面的情景,回答问题:
小王逛超市看到如下两个超市的促销信息

备注:假设两家超市相同的标价都一样.
(1)当一次性购买标价总额是400元时,甲、乙超市实际付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款189元和474元,若他只去一次该超市购买同样多的商品,可以节省多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表:方程1、方程2、方程3…是按照一定规律排列的一列方程:
序号 | 方程 | 方程的解 |
1 |
| x1=3,x2=4 |
2 |
| x1=4,x2=6 |
3 |
| x1=5,x2=8 |
… | … | … |
(1)若方程![]() ﹣
﹣![]() =1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
=1(a>b)的解是x1=6,x2=10,则a=_____b=_____.
(2)请写出这列方程中第n个方程:_____ 方程的解:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E为矩形ABCD的边AB上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为( )

A.5B.6C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鹅岭公园内的小山坡上有一观景楼AB*(如图),山坡BC的坡度为i=1:2.4,为了测量观景楼AB的高度,小楚在山脚C处测得观景楼顶部A的仰角为45°,然后从山脚C沿山坡CB向上行走26米到达E处,测得观景楼顶部A的仰角为72°,(A、B、C、D、E在同一平面内),则观景楼AB的高度约为( )米.(结果精确到0.1米,参考数据: ![]() ,
, ![]() ,
, ![]() )
)

A. 15.6米 B. 18.1米 C. 19.2米 D. 22.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 和
和![]() 中,
中,![]() ,
,![]() .
.

(1)如图1,当点![]() 在对角线
在对角线![]() 上,点
上,点![]() 在
在![]() 边上时,连接
边上时,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() 与
与![]() 的数量关系是_____,
的数量关系是_____,![]() _____
_____![]() ;
;
(2)如图2,将图1中的![]() 绕点
绕点![]() 旋转,使点
旋转,使点![]() 在
在![]() 的延长线上,(1)中的其他条件不变.
的延长线上,(1)中的其他条件不变.
①(1)中![]() 与
与![]() 的数量关系仍然成立吗?请证明你的结论;
的数量关系仍然成立吗?请证明你的结论;
②求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ACB=90°,AC:BC=4:3,O是BC上一点,⊙O交AB于点D,交BC延长线于点E.连接ED,交AC于点G,且AG=AD.
(1)求证:AB与⊙O相切;
(2)设⊙O与AC的延长线交于点F,连接EF,若EF∥AB,且EF=5,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com