
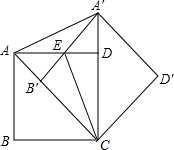
 如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.求证:AA′=CE.
如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.求证:AA′=CE. 分析 根据正方形的性质得AD=CD,∠ADC=90°,∠CAB=45°,则∠A′DE=90°,再根据旋转的性质得∠CA′B′=∠CAB=45°,则∠A′ED=45°,于是可得A′D=DE,然后根据“SAS”可判断△AA′D≌△CED,则根据全等三角形的性质即可得到结论.
解答 证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠A′DE=90°,
∵正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′,
∴∠CA′B′=45°,
∴∠A′ED=45°,
∴A′D=DE,
在△AA′D和△CED中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADA′=∠CDE}\\{A′D=ED}\end{array}\right.$,
∴△AA′D≌△CED(SAS),
∴AA′=CE.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和正方形的性质.


科目:初中数学 来源: 题型:解答题
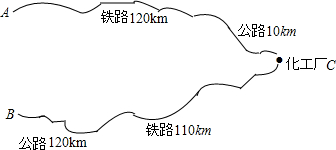 如图,某化工厂C与A、B两地有公路、跌路相连.这家工厂从A地购买一批每吨1000元的原料回工厂,制成若干每吨8000元的产品运回B地.已知公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),若这两次运输共支出铁路运费97200元,且这批产品的销售款比原料费与运输费的和多1887800元.这两次运输共支出公路运输费多少元?
如图,某化工厂C与A、B两地有公路、跌路相连.这家工厂从A地购买一批每吨1000元的原料回工厂,制成若干每吨8000元的产品运回B地.已知公路运价为1.5元/(吨.千米),铁路运价为1.2元/(吨.千米),若这两次运输共支出铁路运费97200元,且这批产品的销售款比原料费与运输费的和多1887800元.这两次运输共支出公路运输费多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,在三角形中已知两边之长分别为a,b(a<b),那么第三边上的中线的长度x的取值范围是$\frac{b-a}{2}$<x<$\frac{b+a}{2}$.
如图所示,在三角形中已知两边之长分别为a,b(a<b),那么第三边上的中线的长度x的取值范围是$\frac{b-a}{2}$<x<$\frac{b+a}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com