练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
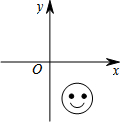
    6．如图，笑脸盖住的点的坐标可能为（　　）
    A．（5，2）B．（-4，-6）C．（3，-4）D．（-2，3）

    分析 先判断出笑脸盖住的点在第四象限，再根据各象限内点的坐标特征对各选项分析判断即可得解．

    解答 解：由图可知，笑脸盖住的点在第四象限，
    A、（5，2）在第一象限，故本选项不符合题意；
    B、（-4，-6）在第三象限，故本选项不符合题意；
    C、（3，-4）在第四象限，故本选项符合题意；
    D、（-2，3）在第二象限，故本选项不符合题意．
    故选C．

    点评 本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    15．矩形的两条对角线的一个夹角为120°，两条对角线的和为4cm，则这个矩形的一条较长边长为$\sqrt{3}$cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．根据下列条件，利用网格点和三角尺画图：
    （1）补全△A′B′C′
    （2）画出AC边上的中线BD；
    （3）画出AC边上的高线BE；
    （4）求△ABD的面积4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

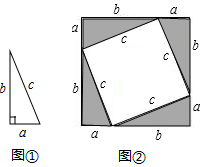    14．用直角边是a，b斜边是c的四个全等直角三角形（图①）拼成②图．
    观察图形并思考，填空：大正方形的面积可表示为：（a+b）2
    （1）这个大正方形的面积还可以怎样表示？c2+2ab
    （2）于是可列等式为（a+b）2=c2+2ab，将等式化简、整理得a2+b2=c2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

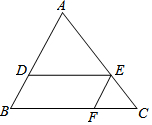    1．如图，在△ABC中，点D，E，F分别在边AB，AC，BC上，且DE∥BC，EF∥AB．若AD=2BD，则$\frac{{S}_{△EFC}}{{S}_{?BFED}}$的值为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

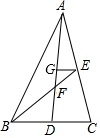    11．如图，在△ABC中，中线AD，BE相交于点F．EG∥BC，交AD于点G，则S△EFG与S△ABC的比为（　　）
    A．$\frac{1}{12}$B．$\frac{1}{18}$C．$\frac{1}{24}$D．$\frac{1}{36}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

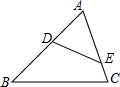    18．在△ABC与△AED中，$\frac{AE}{AB}$=$\frac{AD}{AC}$=$\frac{1}{2}$，则S△ADE：S△ABC的值为（　　）
    A．$1：\sqrt{3}$B．1：2C．1：3D．1：4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．$\frac{2x-1}{3}$-$\frac{5x+1}{2}$≥1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

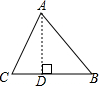    16．如图，在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积．
    某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路，完成解答过程．
    （1）作AD⊥BC于D，设BD=x，用含x的代数式表示CD，则CD=14-x；
    （2）请根据勾股定理，利用AD作为“桥梁”建立方程，并求出x的值；
    （3）利用勾股定理求出AD的长，再计算三角形的面积．

    查看答案和解析>>

    同步练习册答案