
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα=![]() ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα=![]() ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
【问题解决】
(1)请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ=![]() ,求sin2β的值.
,求sin2β的值.

【答案】(1)sin2α=![]() ;(2)sin2β=sin∠MON=
;(2)sin2β=sin∠MON=![]() .
.
【解析】
试题分析:(1)如图1中,⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα=![]() ,可设BC=x,则AB=3x.利用面积法求出CD,在Rt△COD中,根据sin2α=
,可设BC=x,则AB=3x.利用面积法求出CD,在Rt△COD中,根据sin2α=![]() ,计算即可.(2)如图2中,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR⊥NO于点R.首先证明∠MON=2∠Q=2β,在Rt△QMN中,由sinβ=
,计算即可.(2)如图2中,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR⊥NO于点R.首先证明∠MON=2∠Q=2β,在Rt△QMN中,由sinβ=![]() ,设MN=3k,则NQ=5k,易得OM=
,设MN=3k,则NQ=5k,易得OM=![]() NQ=
NQ=![]() ,可得MQ=
,可得MQ=![]() =4k,由
=4k,由![]() MNMQ=
MNMQ=![]() NQMR,求出在Rt△MRO中,根据sin2β=sin∠MON=
NQMR,求出在Rt△MRO中,根据sin2β=sin∠MON=![]() ,计算即可.
,计算即可.
试题解析:(1)如图1中,⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα=![]() ,可设BC=x,则AB=3x.
,可设BC=x,则AB=3x.

∴AC=![]() =
=![]() =2
=2![]() x,
x,
∵![]() ACBC=
ACBC=![]() ABCD,
ABCD,
∴CD=![]() x,
x,
∵OA=OC,
∴∠OAC=∠OCA=α,
∴∠COB=2α,
∴sin2α=![]() =
=![]() .
.
(2)如图2中,连接NO,并延长交⊙O于点Q,连接MQ,MO,过点M作MR⊥NO于点R.

在⊙O中,∠NMQ=90°,
在Rt△QMN中,∵sinβ=![]() ,
,
∴设MN=3k,则NQ=5k,易得OM=![]() NQ=
NQ=![]() ,
,
∴MQ=![]() =4k,
=4k,
∵![]() ,
,
∴3k4k=5kMR
∴MR=![]() ,
,
在Rt△MRO中,sin2β=sin∠MON= .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC. 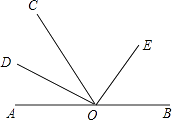
(1)与∠AOE互补的角是 .
(2)若∠AOC=72°,求∠DOE的度数;
(3)当∠AOC=x时,请直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0. ![]()
(1)求A、B两点的坐标;
(2)点C在数轴上对应的数为x,且x是方程2x+1= ![]() x﹣8的解
x﹣8的解
①求线段BC的长;
②在数轴上是否存在点P,使PA+PB=BC?求出点P对应的数;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用有理数的运算研究下面问题.规定:水位上升为正,水位下降为负;几天后为正,几天前为负.如果水位每天下降4cm,那么3天后的水位变化用算式表示正确的是( )
A. (+4)×(+3) B. (+4)×(﹣3) C. (﹣4)×(+3) D. (﹣4)×(﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (m为常数)的图象在一、三象限.
(m为常数)的图象在一、三象限.
(1)求m的取值范围;
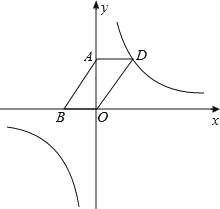
(2)如图,若该反比例函数的图象经过ABOD的顶点D,点A、B的坐标分别为(0,3),(﹣2,0).
①求出函数解析式;
②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为 ;若以D、O、P为顶点的三角形是等腰三角形,则满足条件的点P的个数为 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CECB.
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com