
【题目】如图,在等边△ABC中,M为BC边上的中点,D是射线AM上的一个动点,以CD为一边且在CD的下方作等边△CDE,连接BE. 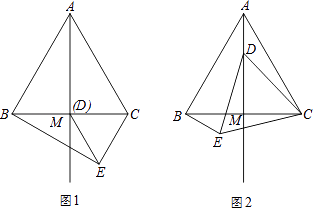
(1)填空:若D与M重合时(如图1)∠CBE=度;
(2)如图2,当点D在线段AM上时(点D不与A、M重合),请判断(1)中结论是否成立?并说明理由;
(3)在(1)的条件下,若AB=6,试求CE的长.
【答案】
(1)30
(2)解:(1)中结论成立.理由如下:
如图2.
∵△ABC和△CDE均为等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠DCB+∠BCE=60°,
∴∠ACD=∠BCE.
在△ACD与△BCE中,
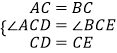 ,
,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∵在等边△ABC中,M是BC中点.
∴∠CAD= ![]() ∠BAC=30°,
∠BAC=30°,
∴∠CBE=30°
(3)解:如图1.
∵在等边△ABC中,AB=6,
∴BC=AB=6.
∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴CD=BD= ![]() BC=3,
BC=3,
∵△CDE是等边三角形,
∴CE=CD=3.
【解析】解:(1)如图1.
∵在等边△ABC中,M为BC边上的中点,D与M重合,
∴BD=CD,
∵△CDE是等边三角形,
∴∠CDE=60°,CD=DE,
∴BD=DE,
∴∠BED=∠DBE,
又∵∠BED+∠DBE=∠CDE=60°,
∴∠DBE=30°,即∠CBE=30°;
所以答案是30;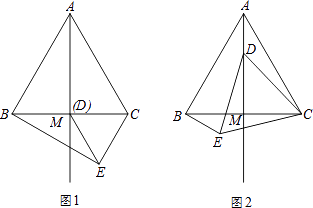
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】全等图形是相似比为1的相似图形,因此全等是特殊的相似,我们可以由研究全等三角形的思路,提出相似三角形的问题和研究方法.这种其中主要利用的数学方法是( )
A.代入法B.列举法C.从特殊到一般D.反证法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AB=AC,D点在AC上,E点在BA的延长线上,BD=CE,BD的延长线交CE于F.证明: 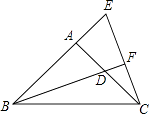
(1)AD=AE
(2)BF⊥CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣![]() ﹣(+13)+(﹣
﹣(+13)+(﹣![]() )﹣(﹣17)
)﹣(﹣17)
(2)﹣22+3÷(﹣1)2017﹣|﹣4|×5
(3)先化简再求值﹣3(2x2﹣xy)+4(x2+xy﹣6),其中x=﹣1,y=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求31+32+33+34+35+36的值
解:设S=31+32+33+34+35+36①
则3S=32+33+34+35+36+37②
用②﹣①得,3S﹣S=(32+33+34+35+36+37)﹣(31+32+33+34+35+36)=37﹣3
∴2S=37﹣3,即S=![]() ,∴31+32+33+34+35+36=
,∴31+32+33+34+35+36=![]()
以上方法我们成为“错位相减法”,请利用上述材料,解决下列问题:
(一)棋盘摆米
这是一个很著名的故事:阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏?阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放八粒…按这个方法放满整个棋盘就行”国王以为要不了多少粮食,就随口答应了,结果国王输了
(1)国际象棋共有64个格子,则在第64格中应放 粒米(用幂表示)
(2)设国王输给阿基米德的米粒数为S,求S
(二)拓广应用:
1.计算:![]() (仿照材料写出求解过程)
(仿照材料写出求解过程)
2.计算:![]() = (直接写出结果)
= (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为三角形ABD中线, 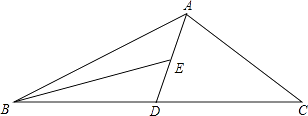
(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)为绿化环境,汇川区园林局引进了A、B两种树苗,若购进A种树苗4棵,B种树苗2棵,需要1600元;若购进3棵A种树苗,4棵B种树苗,需1700元,问:
(1)A、B两种树苗的单价各是多少?
(2)若计划不超过8300元购进A、B两种树苗共30棵,其中计划A种树苗至少比B种树苗的2倍多2棵,问有几种采购方案?那种方案最节约?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com