
【题目】为实现2020年全面脱贫的目标,我国实施“精准扶贫”战略,从而使贫困户的生活条件得到改善,生活质量明显提高.为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,统计发现班上贫困家庭学生人数分别有2名,3名,4名,5名,6名,共五种情况.并将其制成了如下两幅不完整的统计图:
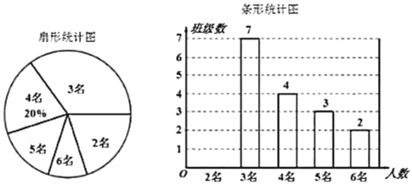
请回答下列问题:
(1)求该校一共有班级________个;在扇形统计图中,贫困家庭学生人数有5名的班级所对应扇形圆心角为________°;
(2)将条形图补充完整;
(3)甲、乙、丙是贫困生中的三名学生,学校决定从这三名学生中随机抽取两名代表到市里进行发言,用列表法或画树状图法,求同时抽到甲,乙两名学生的概率.
【答案】(1)20,54;(2)补图见解析;(3)树状图见解析,![]() .
.
【解析】
(1)根据困家庭学生人数有4名的班级的个数及百分比可求出班级总数,根据贫困家庭学生人数有5名的班级的个数可得贫困家庭学生人数有5名的班级所占百分比,乘以360°即可得对应扇形圆心角的度数;
(2)根据总人数可求出贫困家庭学生人数有2名的班级的个数,据此补全条形图即可;
(3)画出树状图,得出总情况数及同时抽到甲,乙两名学生的情况数,根据概率个数即可得答案.
(1)该校一共有班级:4÷20%=20(个),
贫困家庭学生人数有5名的班级所对应扇形圆心角为:![]() =54°,
=54°,
故答案为:20,54
(2)贫困家庭学生人数有2名的班级为:20-2-3-4-7=4(个),
∴补全条形图如下:
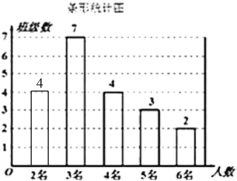
(3)画树状图如下:

由树状图可知:共有6种等可能情况,同时抽到甲,乙两名学生的情况有2种,
∴同时抽到甲,乙两名学生的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 为⊙
为⊙![]() 的直径,点
的直径,点![]() 是半径
是半径![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),
重合),![]() 为⊙
为⊙![]() 的半径,⊙
的半径,⊙![]() 的弦
的弦![]() 与⊙
与⊙![]() 相切于点
相切于点![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() .
.
(1)设![]() ,则
,则![]() 与
与![]() 之间的数量关系是什么?请说明理由.
之间的数量关系是什么?请说明理由.
(2)若![]() ,点
,点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
①当![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②当![]() 时,点
时,点![]() 是弦
是弦![]() 的中点.
的中点.
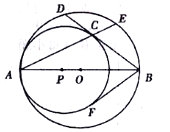
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着国内疫情基本得到控制,旅游业也慢慢复苏,经市场调研发现旅游景点未来![]() 天内,旅游人数
天内,旅游人数![]() 与时间
与时间![]() 的关系如下表;每张门票
的关系如下表;每张门票![]() 与时间
与时间![]() 之间存在如下图所示的一次函数关系.(
之间存在如下图所示的一次函数关系.(![]() ,且
,且![]() 为整数)
为整数)
时间 |
|
|
|
|
|
人数 |
|
|
|
|
|
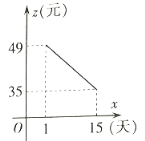
请结合上述信息解决下列问题:
(1)直接写出:![]() 关于
关于![]() 的函数关系式是 .
的函数关系式是 .![]() 与时间
与时间![]() 函数关系式是 .
函数关系式是 .
(2)请预测未来![]() 天中哪一天的门票收入最多,最多是多少?
天中哪一天的门票收入最多,最多是多少?
(3)为支援武汉抗疫,该旅游景点决定从每天获得的门票收入中拿出![]() 元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于
元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
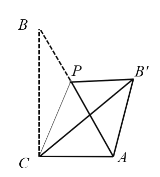
【题目】已知,Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,点P是AB上一点,连接CP,将∠B沿CP折叠,使点B落在B'处.以下结论正确的有________
①当AB'⊥AC时,AB'的长为![]() ;
;
②当点P位于AB中点时,四边形ACPB'为菱形;
③当∠B'PA=30°时,![]() ;
;
④当CP⊥AB时,AP:AB':BP=1:2:3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2-2mx-m2+4m-2的对称轴为l,抛物线与y轴交于点C,顶点为D.
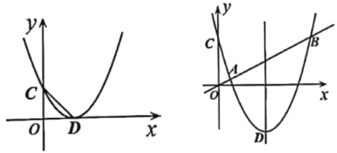
(1)判断抛物线与x轴的交点情况;
(2)如图1,当m=1时,点P为第一象限内抛物线上一点,且△PCD是以PD为腰的等腰三角形,求点P的坐标;
(3)如图2,直线![]() 和抛物线交于点A、B两点,与l交于点M,且MO=MB,点Q(x0,y0)在抛物线上,当m>1时,
和抛物线交于点A、B两点,与l交于点M,且MO=MB,点Q(x0,y0)在抛物线上,当m>1时,![]() 时,求h的最大值.
时,求h的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
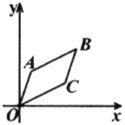
【题目】如图,已知![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() ,若将
,若将![]() 先沿
先沿![]() 轴进行第一次对称变换,所得图形沿
轴进行第一次对称变换,所得图形沿![]() 轴进行第二次对称变换,轴对称变换的对称轴遵循
轴进行第二次对称变换,轴对称变换的对称轴遵循![]() 轴、
轴、![]() 轴、
轴、![]() 轴、
轴、![]() 轴…的规律进行,则经过第2018次变换后,
轴…的规律进行,则经过第2018次变换后,![]() 顶点
顶点![]() 坐标为()
坐标为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
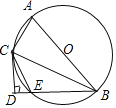
【题目】如图,已知AB是⊙O的直径,BE是⊙O的弦,BC是∠ABE的平分线且交⊙O于点C,连接AC,CE,过点C作CD⊥BE,交BE的延长线于点D.
(1)∠DCE ∠CBE;(填“>”“<”或“=”)
(2)求证:DC是⊙O的切线;
(3)若⊙O的直径为10,sin∠BAC=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
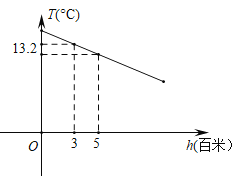
【题目】某地区山峰的高度每增加1百米,气温大约降低0.6℃.气温T(℃)和高度h(百米)的函数关系如图所示.请根据图象解决下列问题:
(1)求高度为5百米时的气温.
(2)求T关于h的函数表达式.
(3)测得山顶的气温为6℃,求该山峰的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
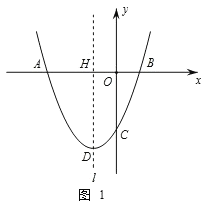
【题目】如图1,已知抛物线![]() 经过A(-3,0),B(1,0),C(0,-3)三点,其顶点为D,对称轴是直线
经过A(-3,0),B(1,0),C(0,-3)三点,其顶点为D,对称轴是直线![]() ,
,![]() 与x轴交于点H.
与x轴交于点H.
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴![]() 上的一个动点,求△PBC周长的最小值;
上的一个动点,求△PBC周长的最小值;
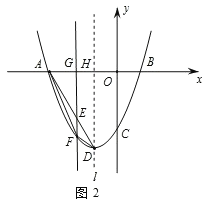
(3)如图2,若E是线段AD上的一个动点(E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①试求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com