
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ![]() ,求BC的长.
,求BC的长.
【答案】
(1)证明:连接OB,如图所示: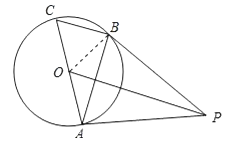
∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠C+∠BAC=90°,
∵OA=OB,
∴∠BAC=∠OBA,
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,
即PB⊥OB,
∴PB是⊙O的切线
(2)解:∵⊙O的半径为2 ![]() ,
,
∴OB=2 ![]() ,AC=4
,AC=4 ![]() ,
,
∵OP∥BC,
∴∠C=∠BOP,
又∵∠ABC=∠PBO=90°,
∴△ABC∽△PBO,
∴ ![]() ,
,
即 ![]() ,
,
∴BC=2
【解析】连接OB,由圆周角定理得出∠ABC=90°,得出∠C+∠BAC=90°,再由OA=OB,得出∠BAC=∠OBA,证出∠PBA+∠OBA=90°,即可得出结论;证明△ABC∽△PBO,得出对应边成比例,即可求出BC的长.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.图1,2,3是旋转三角板得到的图形中的3种情况.
研究:
(1)三角板绕点P旋转,观察线段PD和PE之间有什么数量关系,并结合图2加以证明;
(2)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由;
(3)若将三角板的直角顶点放在斜边AB上的M处,且AM:MB=1:3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合图4加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,在四边形 ABCD 中,AB∥DC,E 是 BC 中点,若 AE 是∠BAD 的平分线,试探究 AB,AD,DC 之间的数量关系,请直接写出结论,无需证明.
(2)如图 2,在四边形ABCD 中,AB∥DC,AF 与DC 的延长线交于点F,E 是BC 中点,若AE 是∠BAF 的平分线,试探究AB,AF,CF 之间的数量关系,证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6cm的⊙O中,点A是劣弧 ![]() 的中点,点D是优弧
的中点,点D是优弧 ![]() 上一点,且∠D=30下列四个结论:①OA⊥BC;②BC=
上一点,且∠D=30下列四个结论:①OA⊥BC;②BC= ![]() cm;③cos∠AOB=
cm;③cos∠AOB= ![]() ;④四边形ABOC是菱形.其中正确结论的序号是( )
;④四边形ABOC是菱形.其中正确结论的序号是( )
A.①③
B.①②③④
C.①②④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求,解答下列问题.
(1)解下列方程组(直接写出方程组的解即可):
A.![]() B.
B.![]() C.
C.![]()
方程组A的解为 ,方程组B的解为 ,方程组C的解为 ;
(2)以上每个方程组的解中,x值与y值的大小关系为 ;
(3)请你构造一个具有以上外形特征的方程组,并直接写出它的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,过点A作AD⊥BC,垂足为D,E为AB上一点,过点E作EF⊥BC,垂足为F,过点D作DG∥AB交AC于点G.
(1)依题意补全图形;
(2)请你判断∠BEF与∠ADG的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下面证明过程补充完整:
已知:如图,∠ADC=∠ABC,BE、DF分别平行∠ABC、∠ADC,且∠1=∠2.
求证:∠A=∠C.
证明:因为BE、DF分别平分∠ABC、∠ADC,( ).
所以∠1=![]() ∠ABC,∠3=
∠ABC,∠3=![]() ∠ADC( ).
∠ADC( ).
因为∠ABC=∠ADC(已知),
所以∠1=∠3( ),
因为∠1=∠2(已知),
所以∠2=∠3( ).
所以 ∥ ( ).
所以∠A+∠ =180°,∠C+∠ =180°( ).
所以∠A=∠C( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+k+2与x轴的公共点有两个.
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的公共点A和B的坐标及顶点C的坐标;
(3)观察图象,当x取何值时y>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com